場合の数①　樹形図の書き方

場合の数とは

場合の数とは、「～になるのは何通りあるか。」を求める問題です。
「クラスの中から委員長と副委員長を選ぶのは何通りの組み合わせがあるか。」や、「クラスからリレーの選手を3人選ぶには何通りの組み合わせがあるか。」など、身近な所にもよく出てくる考え方です。もちろん、「夏目さんと芥川さん」、「伊坂さんと東野さん」という具合に、すべての組み合わせを数え上げていけば良いのですが、場合の数の問題では、答えが100や1000、時には10万を越すこともあるので、工夫をして考えていかなければなりません。

樹形図の書き方

場合の数の解き方の工夫ということで、一番最初に考えるのは樹形図です。樹形図は、枝分かれをさせていき、どんな組み合わせがあるかを見やすく書いた図です。次の例題を使いながら書き方を考えていきましょう。

（例題1）

1,2,3,4と書かれたカードが1枚ずつあります。この中から2枚引いて、2ケタの整数を作ります。何通りの整数ができるでしょう。

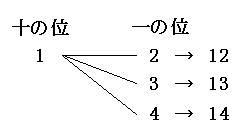
試しに、すべての組み合わせを書き出してみましょう。

答えは12通りと出てしまいましたが、もう少ししっかりと考えてみます。
今回、十の位が「1」のものを赤い□で囲っています。この3つはどれも十の位が「１」だから、そんなに何度も「1」を書かなくてもいいじゃないかと思うわけです。その手間をはぶけるのが樹形図です。次のように書きます。

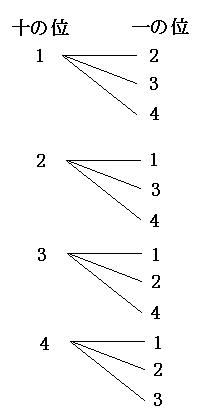
これで十の位の「1」は、一回だけしか書かなくてよくなります（サボれます）。では、十の位が「2」のときも、「3」のときも、「4」のときも書いてみましょう。

よって答えは

12通り

今回は2ケタだったのであまりサボれませんでしたが、枝分かれが多くなってくると便利さがわかってくると思います。

（例題2）

4人のチームの中で、リレーの走る順番を決めます。何通りの順番があるでしょう。

4人に名前がついていないので、名前をつけておきます。今回は「aさん」「bさん」「cさん」「dさん」とします。（自分の好きな名前をつけて大丈夫です。ただ、樹形樹を書く時に面倒くさくなるので、画数の多いものはおすすめしません。）
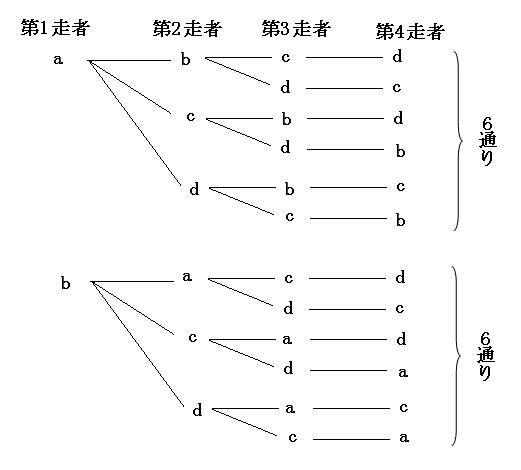
それでは樹形図を書いてみます。

樹形図を書いてみると言いながら、第１走者が「aさん」のときと、「bさん」のときまでしか書いていません。しかし、この先は書かなくても同じパターンが続くことは分かりますので、ここまででサボりました。

第一走者がcさんのときも6通り、dさんのときも6通りあるので、

6通り×4＝24通り

よって答えは

24通り

樹形図は、人が書いているのを見ていると簡単に書けるように見えますが、自分で書いてみると意外と書けなかったりするので、必ず自分の力だけで書いてみてください。樹形図を自分の力で書けないと、次に説明する内容がサッパリ訳が分からなくなってしまいますので、なにとぞよろしくお願いします。
それでは樹形図の書き方をまとめます。

まとめ

場合の数の樹形図を書くときは