場合の数②　計算で求める

場合の数を計算で求めるには

前のページで樹形図の書き方を学習しましたが、樹形図を書かずに、計算だけで場合の数を求めることができます。樹形図は非常に分かりやすく便利なのですが、答えが「30通り」を超えた辺りから書くのがしんどくなります。計算だけで出せれば、それはもうとっても楽です（サボれます）。
ですが、計算で求めるためには、樹形図をしっかりと理解していなくてはいけません。なので、樹形図を書く練習をしっかりとやってから計算での求め方を学習しましょう。（ここはサボれない）

場合の数の計算方法

それでは、場合の数の計算方法を、次の例題を解きながら考えてみましょう。

（例題1）

1,2,3,4と書かれたカードが1枚ずつあります。この中から3枚引いて、3ケタの整数を作ります。何通りの整数ができるでしょう。

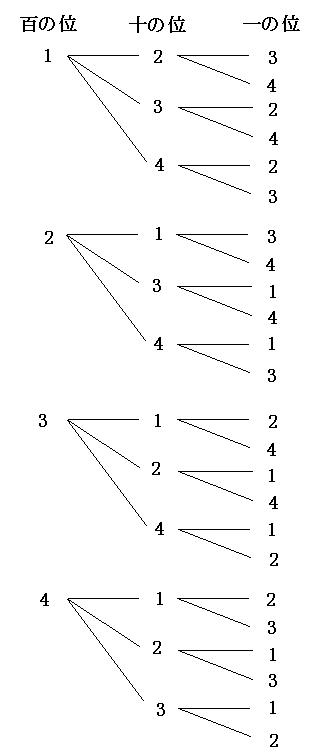
今回は説明のために樹形図を書いてみます。

ということで、答えは24通りなのですが、もう少し考えてみましょう。
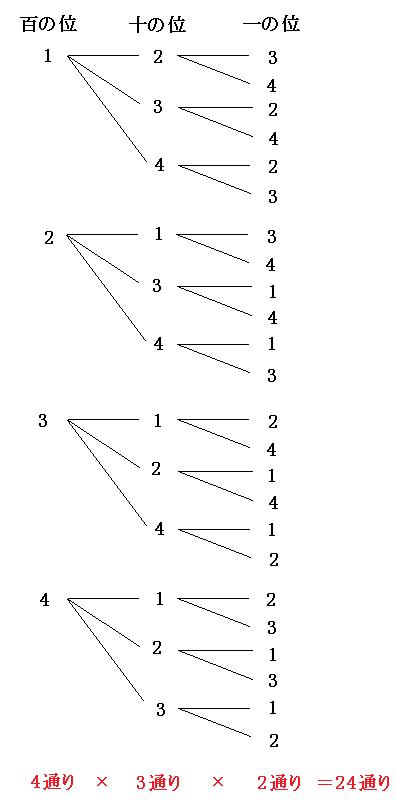
枝分かれの様子から考えて、かけ算の式を作ってみましょう。
百の位が4通りあって、そこから十の位に向けて全て3つに枝分かれしています。さらに十の位から一の位に向けて、全て2つに枝分かれしています。
つまり一の位までに出来上がる枝の数は、4×3×2＝24本になります。

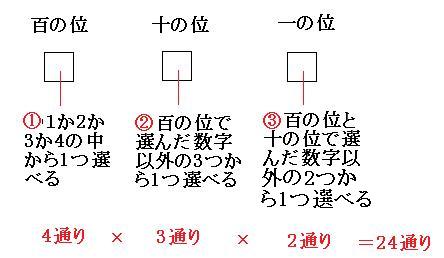
つまり、樹形図を書かなくても、以下のように考えることもできます。

よって答えは

24通り

このかけ算が使えるようになると、場合の数はグッと楽になりますし、1万通りや10万通りの場合も求められるので、可能性が広がります。

（例題2）

1から9までの整数を1回ずつ使って、9ケタの整数をつくります。何通りの整数ができるでしょう。

樹形図を書いてみるとわかりますが、たぶん5秒位で挫折すると思います。計算を使わなければ解けない問題です。

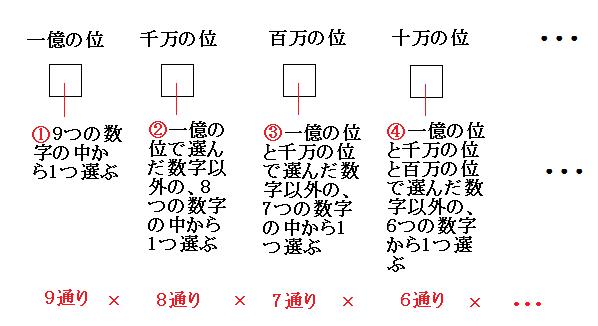
上の図は途中までしか書いていませんが、この先も同じように続くので、

9×8×7×6×5×4×3×2×1
＝362880

よって答えは

362880通り

樹形図を書いたらすごいことになりそうですね！！

条件付きの場合の数の計算方法

場合の数の問題では、「ここにはこれを入れなければならない」とか、「ここにはこれを入れてはいけない」などの、条件のついたものがあります。
このような条件がついている場合、条件がついている部分を優先して考えていきます。

（例題3）

0,1,2,3,4と書かれたカードが1枚ずつあります。この中から3枚引いて3ケタの整数を作るとき、次の問いに答えましょう。

（1）全部で何通りの整数ができるでしょう。

（2）何通りの奇数ができるでしょう。

（3）何通りの偶数ができるでしょう。

（1）全部で何通りの整数ができるでしょう。

ウッカリすると例題1と同じようにできるじゃないかと思うのですが、3ケタの整数を作らなくてはならないので、百の位に「0」のカードを使うことはできません。
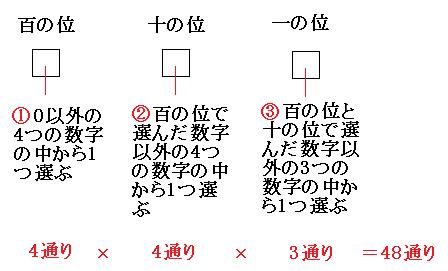
つまり、この問題には「百の位には0を入れてはいけない」という条件がついているのです。 百の位に条件がついているので、百の位を優先して考えます。

よって答えは

48通り

（2）何通りの奇数ができるでしょう。

何ケタの数字でも、一の位が奇数ならばその数字は奇数になります。
つまり、今回の条件は、「百の位には0を入れてはいけない」に加えて、「一の位は奇数でなければいけない」です。奇数のカードは「1」か「3」しかないので、「一の位は1か3でなければいけない」です。
百の位と一の位に条件がついていますが、この場合は必ず一の位を優先して考えます。次に百の位、最後に十の位の順番で考えます。
一の位を一番最初に考える理由は、条件を複雑にさせないためです。
百の位には「1, 2, 3, 4」のカードが選べます。一の位には「1, 3」のカードが選べます。
百の位を先に決めてしまうと、例えば、「1」を選ぶか「2」を選ぶかで、一の位の条件が変わってしまいます。百の位で「1」を選べば、一の位は「3」の1枚しか選べません。ところが、百の位で「2」を選ぶと、一の位は「1」か「3」の2枚の中から選べます。
逆に一の位を先に決めると、一の位で「1」を選んだ場合、百の位では「2, 3, 4」の3枚の中から選ぶことになりますし、一の位で「3」を選んだ場合、百の位では「1, 2, 4」の3枚の中から選ぶことになり、条件が変わりません。
この考え方を理解することはとても重要なことですが、どうしても難しいようならば「○ケタの整数は何通りでしょう系の問題で、偶数や奇数の条件がある場合は、一の位を一番優先して考える」と覚えてしまっても良いと思います。
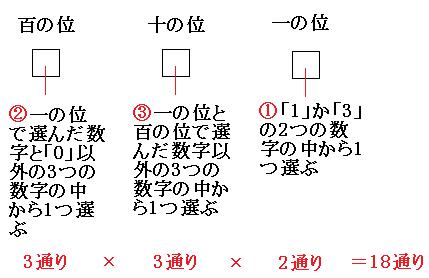
ということで、今回の優先順位は「①一の位、②百の位、③十の位」の順番です。

よって答えは

18通り

（3）何通りの偶数ができるでしょう。

今回の条件は、「百の位には0を入れてはいけない」と、「一の位は0か2か4でなければいけない」です。こちらも一の位を一番優先して考えるのですが、残念ながら、それでも条件が複雑になってしまいます。
一の位で「0」を選んだ場合、百の位は「1, 2, 3, 4」の4枚の中から選べます。
一の位で「2」を選んだ場合、百の位は「1, 3, 4」の3枚の中からしか選べません。
ということで今回は、「一の位で0を選んだとき」と、「一の位で2か4を選んだとき」の2種類を考えていきます。
どちらも優先順位は「①一の位、②百の位、③十の位」の順番です。

一の位が0のときが12通り、一の位が2か4のときが18通りなので、合わせて、

12通り＋18通り＝30通り

よって答えは

30通り

ちなみに、この例題3の（3）には、元も子もないような裏技があります。ポイントは、今回できる3ケタの整数は偶数か奇数しかないということです。
（1）で3ケタの数字は48通りできると分かりました。（2）で奇数が18通りできることがわかりました。奇数でなければ偶数。つまり残りの48通り－18通り＝30通りが偶数です。
このように「○○でなければ、残りは全部□□」のような考え方は、場合の数では結構重要ですし、覚えておくと裏技も見つけやすいです（サボれます）。
それでは、計算で求める場合の数をまとめます。

まとめ

場合の数を計算で求めるときは