場合の数④ 図形と場合の数
図形問題と見せかけて場合の数
問題に三角形や円などが出てきて、「あー、これ図形問題だ。」と構えていると、「はい!実は場合の数の問題でしたー!」っていうひっかけ問題があります。ひっかからないようにしましょう。 パターンはそれほど多くないので、一度ひっかかっておけば、次からは大丈夫だと思います。
円と三角形(または四角形)
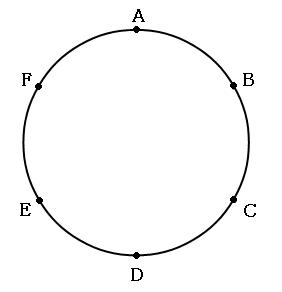
円周上に点がいくつかあって、その点を頂点とする図形は何通りできるかを求める問題です。
(1)何通りの三角形ができるでしょう。
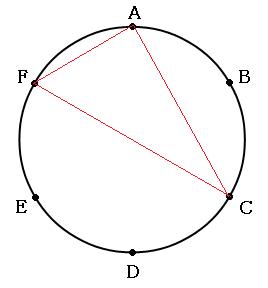
円や三角形が出てくるので、図形の問題かなと思いがちですが、完全に組合せの問題です。 6つの点の中から3つを選べば、自動的に三角形1つが出来上がるのです。例えば「A、C、F」の3点を選ぶと、下のような三角形が出来上がります。
別の3点を組み合わせれば、別の三角形が出来上がります。つまり、何通りの三角形ができるかを聞いていると見せかけて、6つの点から3つを選ぶ組合せは何通りなのかを聞かれているのです!
ということで、さっそく計算しましょう。(樹形図を書いて考えてもOKです。)
6×5×4÷(3×2)=20通り
(組合せの計算方法はこちら)
よって答えは
20通り
(2)何通りの正三角形ができるでしょう。
「もうひっかからないよ!これも場合の数でしょ!」と、思ったでしょう。こちらはほぼ図形問題です。
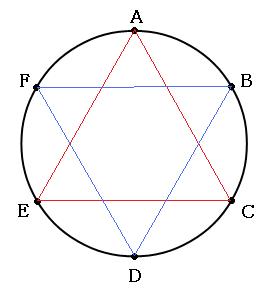
実際にいくつか三角形を書きこんでいくと気づくのですか、正三角形は以下の2種類しか作れません。
なんだか魔法が出てきそうな模様になってしまいましたが、赤い正三角形と青い正三角形が見えるでしょうか?
よって答えは
2通り
直線と三角形
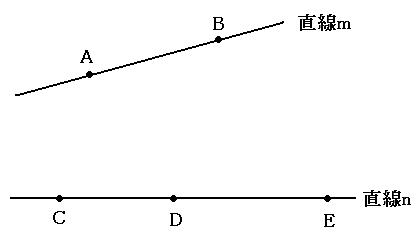
先ほどは円周上に点をとりましたが、今回は直線上に点をとります。多くの場合、直線は2本出てきます。
この問題も、3点を選んでしまえば勝手に三角形ができるので、組合せの問題となります。
ただ、頂点は3ヶ所なので、少し考えなくてはならないことがあります。
直線mから1つの点を選んだとすると、直線nから2つの点を選ぶことになります。逆に、直線nから1つの点を選ぶと、直線mから2つの点を選ぶことになります。
つまり今回は、①「mから1つ、nから2つ」と、②「mから2つ、nから1つ」の2パターンを考えることになります。
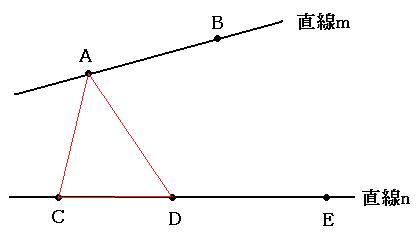
では、さっそく①「mから1つ、nから2つ」のパターンから考えていきましょう。
上の図は、例えば「mから点A、nから点Cと点D」を選んだ場合です。直線mから点Aを選んだとすると、直線n上の3つの点から2つを選ぶことになるので、その組合せは、
3通り×2通り÷2=3通り
直線mから点Bを選んだ場合も、同じように考えて3通りです。よって、
①「mから1つ、nから2つ」の場合は、
3通り+3通り=6通り
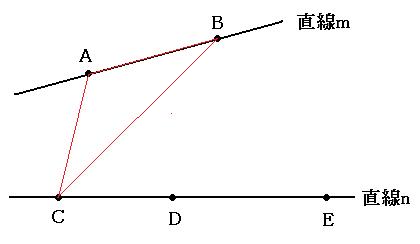
上の図は、例えば「mから点Aと点B、nから点C」を選んだ場合です。というか、直線nから点Cを選んだ場合は、この1通りしか三角形は作れません。
直線nから点Dを選んだときも、点Eを選んだ時も同じなので、
②「mから2つ、nから1つ」の場合は、
1通り×3=3通り
なので、①のパターンと②のパターンを合わせて、
6通り+3通り=9通り
よって答えは9通り
いくつか試しに三角形を書きこんでみながら、「あれやこれや」と考えてみてもいいと思います。この例題2の問題くらいなら、たった9通りですし、全部の三角形を書けてしまいそうですね。
平行線と平行四辺形
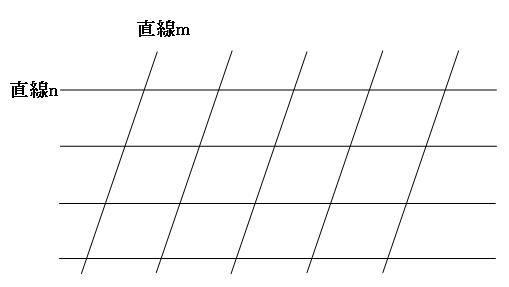
2種類の平行線が何本か引いてあって、平行四辺形は何通り作れるかと問われる問題です。 平行とか平行四辺形とかが登場しますが、完全に組合せの問題です。
完全に組合せの問題です。安心してください(?)。直線mに平行な直線から2本、直線nに平行な直線から2本選べば、自動的に1つ平行四辺形ができあがります。
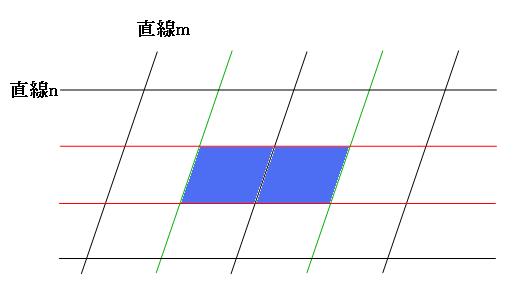
上の図は、例として、直線mに平行な直線から2本(緑の直線)を選び、直線nに平行な直線から2本(赤の直線)を選ぶと、1つの平行四辺形(青い平行四辺形)ができあがる様子です。
よって今回は、直線mに平行な直線5本の中から2本を選び、さらに直線nに平行な直線4本の中から2本を選ぶ、組合せの問題です。
5つの中から2つを選ぶ組合せは、
5通り×4通り÷2=10通り
4つの中から2つを選ぶ組合せは
4通り×3通り÷2=6通り
より、できる平行四辺形の数は、
10通り×6通り=60通り
よって答えは60通り
「あれ?最後の(10通り×6通り=60通り)って、なんでかけ算するの?たし算じゃないの?」と思った方は、もう少し樹形図を書く練習をしましょう。
樹形図が横につながっていく場合はかけ算です。
もうひとつ新しい樹形図を書き始めなくてはいけないときはたし算です。
この違いを理解することはとても大事です。イメージができるようになるまで、たくさん樹形樹を書いて練習してください。
それでは、図形と場合の数をまとめます。
場合の数はもう少し続きます。次は道順を考えます。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!