場合の数⑤ 道順
道順の求め方
今回取り上げるのは、「AからBまで遠回りをせずに行くと、何通りの経路があるでしょう。」という感じの問題が、下のような図と一緒に出題されるものです。
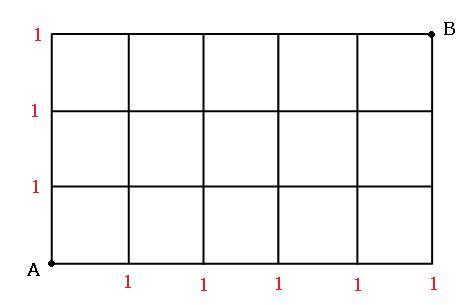
この図で、AからBまでの経路を考えるとき、必ず右に進むか、上に進むかしかできません。下や左に進んでしまうと、遠回りになってしまいます。
それを頭に入れた上で、そこに行くには何通りあるか、どんどん図に書きこんでいきます。
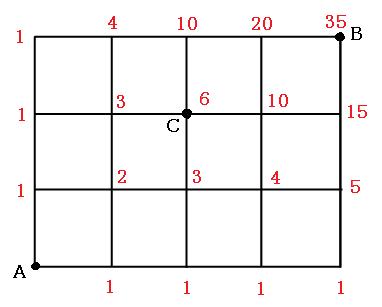
この図では、真っ直ぐ右に進むか、真っ直ぐ上に進む場合は1通りしかありません。なので、まずは「真っ直ぐ進むのは1通りだよ」と、図に書きこんでいきます。
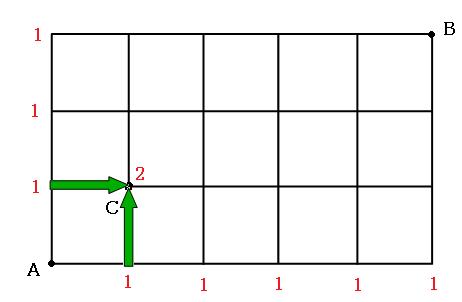
続いて、内側を考えていきます。その場所に行くには何通りあるか、足していきます。スタートに近い方から書いていくと良いです。
例えば、上の図のCの点について考えてみます。Cに行くには、Cの左側から来るか、下側から来るかしかありません。 どちらの場所にも「1」と書かれていますので、Cに行く方法は、1通り＋1通り＝2通りということになります。なので、Cには「2」と書きこんでおきます。他の場所にもどんどん書きこんでいきましょう。 この図においては、左の数字と下の数字を足せばよいのだと思っても大丈夫です。
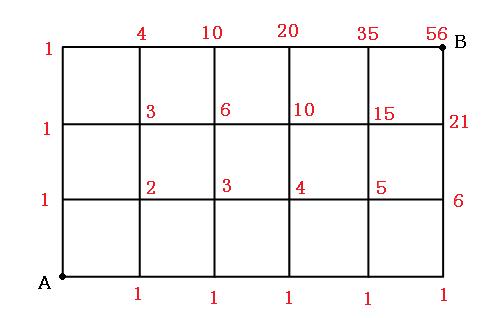
よって、AからBまでは、56通りの経路があるということになります。
どんな形が出てきても、「この場所に行くには何通り？」と考えながらたし算をしていけば必ず求められますので、コツコツと数字を書きこんでいってください。
ここを通るとき、ここを通らないとき
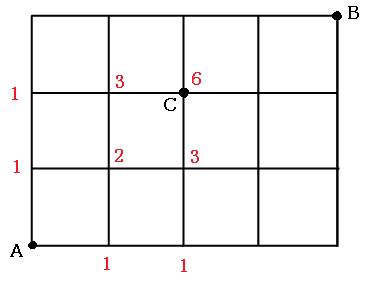
道順の問題を解いていると必ず聞かれるのが、「Aから、Cを通って、Bへ行く経路は何通り？」というタイプの問題です。
この場合は、先ほどと同じように解けるので、数字を書きこんでいってください。
「Aから、Cを通らずに、Bへ行く経路は何通り？」というタイプの問題は、全部の経路から、Cを通る場合をひき算をして解いていきます。
（1）経路は全部で何通りでしょう。
（2）Cを必ず通るとき、経路は何通りでしょう。
（3）Cを通らないとき、経路は何通りでしょう。
（1）経路は全部で何通りでしょう。
先ほどと同じように、数字を入れていきましょう。
よって答えは
35通り
（2）Cを必ず通るとき、経路は何通りでしょう。
同じように数字を入れていくのですが、まずはAからCまでの経路を出していきます。
続けて、CからBまでの経路を書き加えていきましょう。
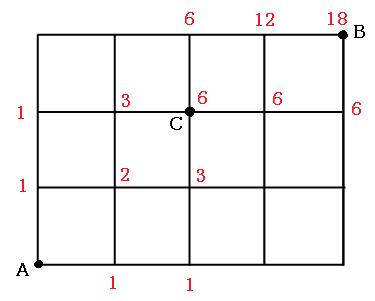
よって答えは
18通り
（3）Cを通らないとき、経路は何通りでしょう。
Cを通らないということは、全部の経路から、Cを通る経路を引けばよいので、
35通り－18通り＝17通り
よって答えは
17通り
はじめは時間がかかるかもしれませんが、練習問題を解いていくうちに、パパっと数字を入れられるようになります。一度できるようになってしまえばあとは簡単に解けますので、頑張って練習してください。
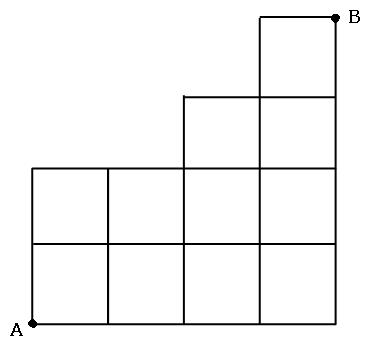
長方形ではないとき
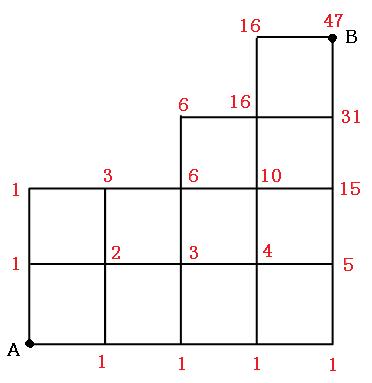
ここまではすべて長方形でしたが、長方形でなくても求められます。やり方も変わりません。同じように数字をコツコツと入れていきましょう。
「あわわ。いつもと違う形が出てきたどうしよう！！」と思うかもしれませんが、安心してください。この場合もただ数字を書きこんでいくだけです。
47通り
例題2が解けないようならば、まだ数字の書きこみ方が定着していないのでしょう。もう少し長方形のやつを練習してからトライしましょう。
例題2が解けるようならば、もうどんな形で出題されても大丈夫でしょう！
それでは道順の場合の数をまとめます。
ここまでで場合の数のお話はおしまいです。次は規則性のお話です。
- 受験生応援オリジナルグッズ
エデュサポオリジナル受験生応援グッズ販売中！
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生！！
