売買損益
売買損益とは
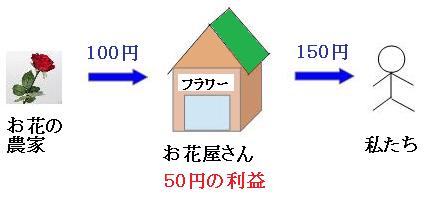
売買損益は、漢字の通り「売る」「買う」「損をする(損失)」「利益が出る」という問題です。 例えばお花屋さんは、お花を作っている農家から花を安く買って、それを少し高くして私たちに売ることで利益を得ます。 農家から買った値段より安くして売ってしまうと、損をしてしまうということになります。
定価 売値 利益の求め方
売買損益の問題では、割合の計算を使うことが多くなります。必ず割合の計算問題を理解してから取り組んでください。
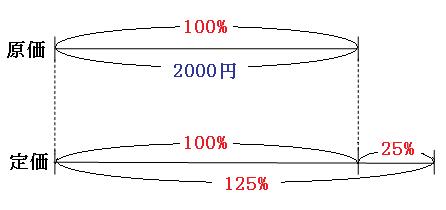
まずは定価がいくらなのか出します。原価をもとにする量として、線分図を書いて考えてみましょう。
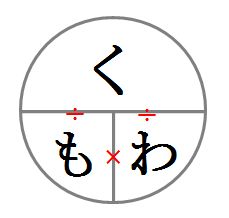
図のように、定価は原価の100%よりも25%多くなって、125%にあたるのが見えると思います。くもわの公式を使うと、
もとにする量×割合=比べられる量
2000円×1.25=2500円
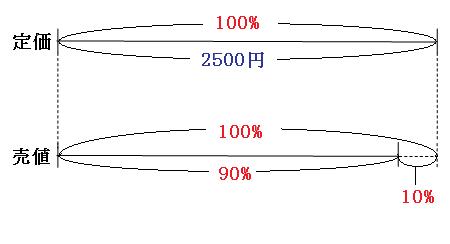
よって、定価が2500円であることがわかりました。続いて売値を出していきます。今度は今出した定価をもとにする量として、線分図を書いてみます。
図のように、売値は定価の100%よりも10%少なくなって、90%にあたるのが見えると思います。くもわの公式を使うと、
もとにする量×割合=比べられる量
2500円×0.9=2250円
よって、売値は2250円です。原価2000円で仕入れてきたものを、売値2250円で売ったので、
2250円-2000円=250円
で、250円の利益が出たことがわかります。よって答えは
250円
問題文に出てくる25%や10%をそのまま式に使うのではなく、「100%から25%増えたから125%」や、「100%から10%へっているから90%」という考え方は非常に重要です。
この考え方は、お店のセールでよく見かける「20%OFF」や、「3割引き」などの計算でも使えます。
ショッピング中に見かけたら、「20%OFFだから、100%から20%へって、80%で計算すればいいんだ!」とか、「3割引きだから、10割から3割へって、7割で計算すればいいんだ!」と、頭の中で計算してみてください。
実際のお値段を計算してみると、さらに良いと思います!
また、売買損益の問題では「もとにする量」がコロコロ変わることもあるので、今は何をもとにする量にしているのか、気をつけながら式を作ってください。
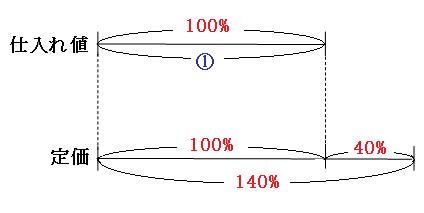
例題1のように、まずは仕入れ値(原価)をもとにする量として考えていきたいのですが、その肝心の仕入れ値がいくらだかわかりません。 仕方がないので、仕入れ値を①として、仕入れ値をもとの量にした線分図を書いていきます。
定価は原価の100%より40%多くなって、140%にあたることがわかるので、くもわを使って、
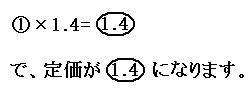
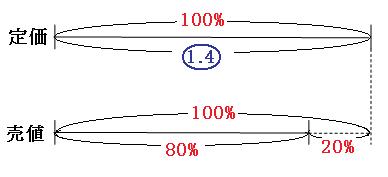
続いて、定価をもとの量にして線分図を書くと、
売値は定価の100%より20%少なくなって、80%になるので、くもわを使って、

比べられる量÷割合=もとにする量
300円÷0.12=2500円
よって答えは
2500円
「○%増し」や「○%引き」の計算は、線分図を書かなくても、頭の中でイメージできるようになるまで練習しましょう。 それでは売買損益の問題をまとめます。
お金の計算はとっても大事です!お金はとっても大事です! 次は和差算です。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!