分配算の練習問題
分配算の練習問題
こちらは、分配算の練習問題を載せているページです。
分配算の詳しい解説はこちらへどうぞ。
分配算は線分図を書いてから、①にあたる数量を求めていきます。(線分図についてはこちら)
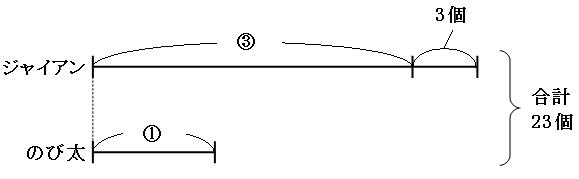
線分図を書いてみましょう。
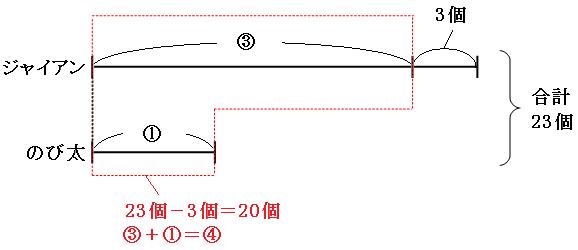
出っ張っている部分を除いて考えると、
赤い四角の中は、
あめ玉の個数
23個-3個=20個
比
③+①=④
④があめ玉20個にあたることが分かりました。なので、①にあたるあめ玉の個数は、
20個÷④=5個
①が5個にあたることが分かったので、これを元にジャイアンくんとのび太くんがもらったあめ玉のそれぞれの個数を求めましょう。
ジャイアンくん
5個×③+3個=18個
のび太くん
5個×①=5個
よって答えは
ジャイアンくん・・・18個、のび太くん・・・5個
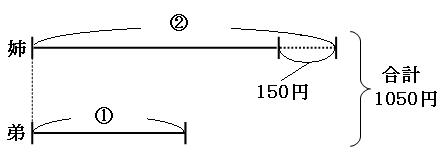
線分図を書いてみましょう。
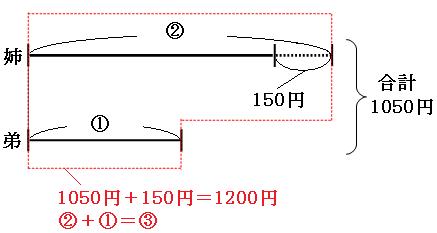
へこんでいる部分も合わせて考えると、
赤い四角の中は、
金額
1050円+150円=1200円
比
②+①=③
③が1200円にあたることが分かりました。なので、①にあたる金額は、
1200個÷③=400円
①が400円にあたることが分かったので、これを元に姉と弟の分けまえを求めましょう。
姉
400円×②-150円=650円
弟
400円×①=400円
よって答えは
姉・・・650円、弟・・・400円
まずは連比の計算をして、3人のジュースの量の比を求めます。(連比の計算方法はこちら)
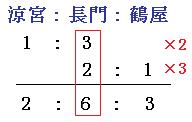
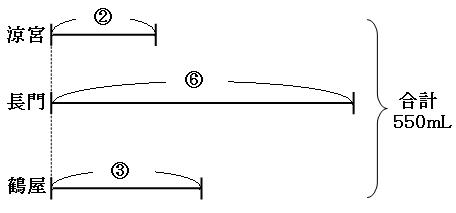
よって、涼宮さんと長門さんと鶴屋さんのジュースの量の比は2:6:3です。それでは線分図を書いてみましょう。
出っ張っている部分はありませんので、そのまま全体を考えて、
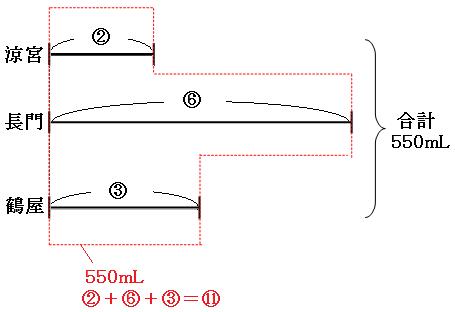
赤い四角の中は、
ジュース
550mL
比
②+⑥+③=⑪
⑪が550mLにあたることが分かりました。なので、①にあたるジュースの量は、
550mL÷⑪=50mL
①が50mLにあたることが分かったので、これを元に3人のジュースの量を求めましょう。
涼宮さん
50mL×②=100mL
長門さん
50mL×⑥=300mL
鶴屋さん
50mL×③=150mL
よって答えは
涼宮さん・・・100mL、長門さん・・・300mL、鶴屋さん・・・150mL
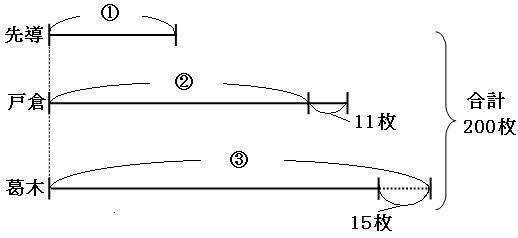
線分図を書いてみましょう。
出っ張っている部分は除いて、へこんでいる部分は合わせて考えると、
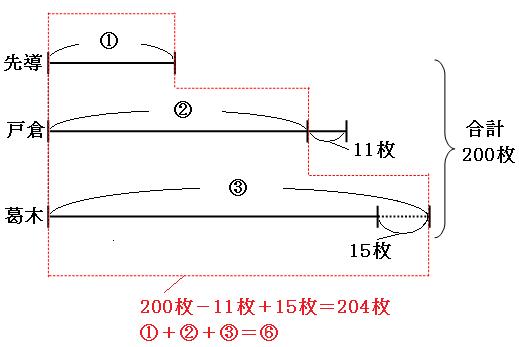
赤い四角の中は、
カード
200枚-11枚+15枚=204枚
比
①+②+③=⑥
⑥が204枚にあたることが分かりました。なので、①にあたるカードの枚数は、
204枚÷⑥=34枚
①が34枚にあたることが分かったので、これを元に3人のカードの枚数を求めましょう。
先導くん
34枚×①=34枚
戸倉さん
34枚×②+11枚=79枚
葛木くん
34枚×③-15枚=87枚
よって答えは
先導くん・・・34枚、戸倉さん・・・79枚、葛木くん・・・87枚
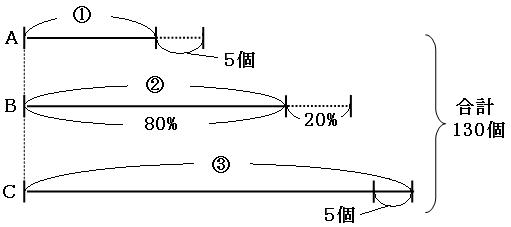
線分図を書いてみましょう。Bの20%は取り除かれましたが、ピンポン球の合計は取り除く前の130個で書いておきます。
今回合計として書いてあるのは、Bのつぶれていたピンポン球を取り除く前の個数です。なので、取り除く前のBの比を求めましょう。 線分図を見ると、②が80%にあたるので、もとにする量を求めると、(割合の計算方法はこちら)
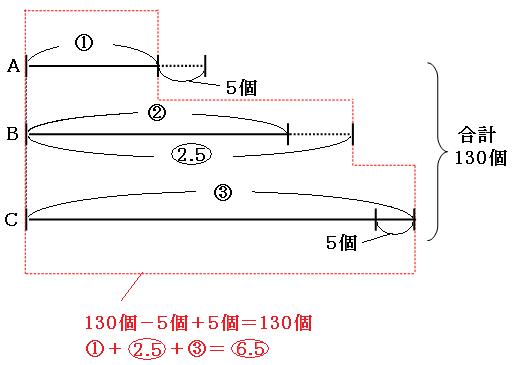
これを、さっきの線分図に書き加えて考えると、
赤い四角の中は、
ピンポン球
130個-5個+5個=130個
①が20個にあたることが分かったので、これを元に、3つの箱の中に最初に入っていたピンポン球の個数を求めましょう。
A
20個+5個=25個
B
20個×②÷0.8=50個
C
20個×③-5個=55個
よって答えは
A・・・25個、B・・・50個、C・・・55個
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!