図形の平行移動
図形の平行移動とは
平行移動とは、図形を同一方向に一定の距離移動させることです。 中学受験の算数では、真横に移動することが多いです。
図形の平行移動の問題の解き方
図形の平行移動の問題で最もよく出題されるのは、重なった部分の面積を求める問題です。
他にもいくつか出題パターンがあるのですが、つまずきやすいのはこの面積を求める問題です。
コツは、前のページで学習した図形上の点の移動と同じです。
時間の経過とともに、重なった部分がどのように変化していくのか、しっかりと頭の中で想像することです。
節目のシーンの図を書いていくのも良いです。
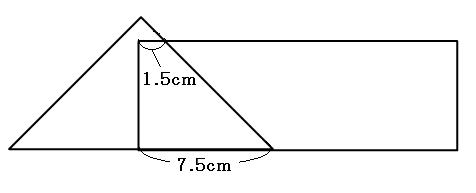
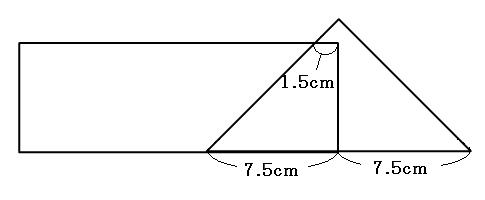
(1)3秒後、ふたつの図形が重なっている部分の面積は何cm²でしょう。
(2)ふたつの図形が重なっている部分が台形になるのは、何秒後から何秒後まででしょう。
(3)ふたつの図形が重なっている部分の面積が0.18cm²になるのは何秒後でしょう。
(4)ふたつの図形が重なっている部分の面積が27cm²になるのは何秒後でしょう。
(1)3秒後、ふたつの図形が重なっている部分の面積は何cm²でしょう。
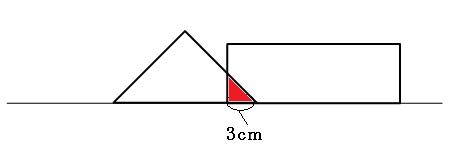
この問題では時間が指定されているので、その時の様子を図に書いてみると簡単です。図形は毎秒3cmの速さで動いているので、3秒間で9cm進みました。
直角三角形を右に9cm平行移動させてみましょう。
重なった部分は、上の図の赤い三角形の部分になります。底辺が3cmになることはすぐに分かるのですが、このままでは高さがわかりません。
が、実はこの赤い三角形は直角二等辺三角形です。「90°、45°、45°」ですので。
なので、高さも3cmです。これを使って面積を求めると、
3cm×3cm÷2=4.5cm²
よって答えは
4.5cm²
(2)ふたつの図形が重なっている部分が台形になるのは、何秒後から何秒後まででしょう。
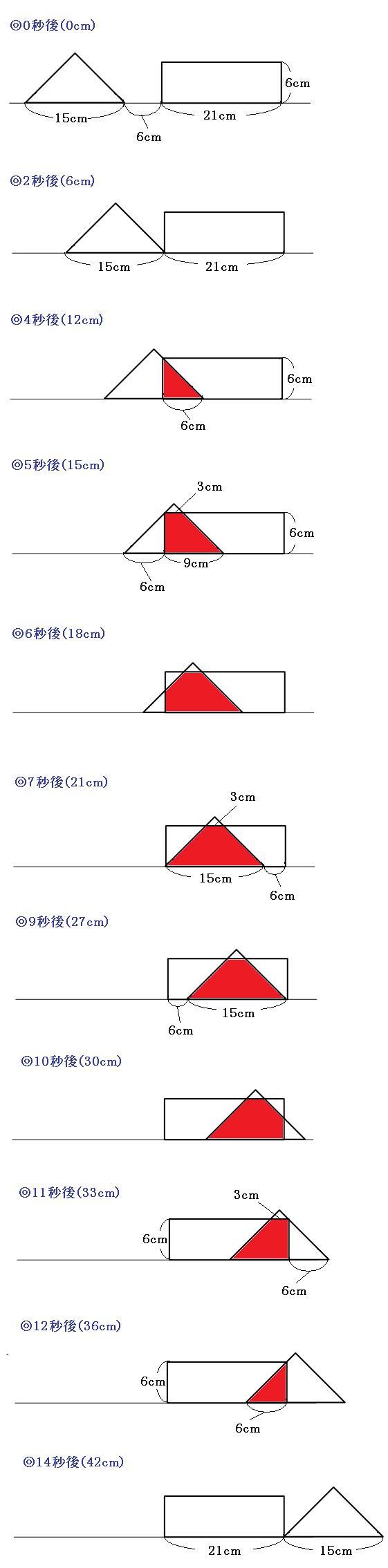
それでは、時間とともに重なった部分がどんなふうに変わっていくか書いていきましょう。
節目となる時間を書いていくとわかりやすいです。
経過がわかるように、節目ではない時間(5秒後と10秒後)も書いておきました。形が頭の中で想像できるようなら、このふたつは書く必要はありません。
図を見ればわかるとは思いますが、念のため、時間ごとに重なっている部分の形と面積についてまとめておきます。
◎0秒後~2秒後
ここではまだ図形は重なりません。
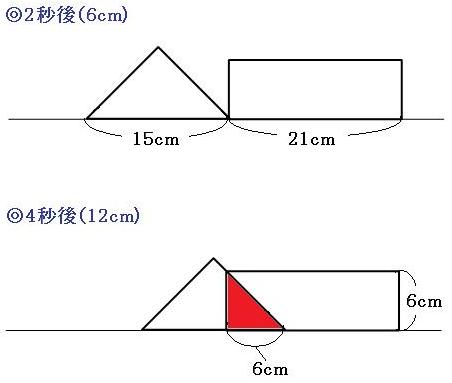
◎2秒後~4秒後
重なった部分は直角二等辺三角形で、面積はだんだん大きくなっていきます。
2秒後→0cm²
4秒後→18cm²
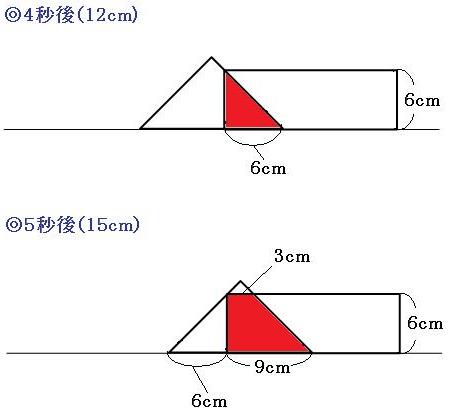
◎4秒後~5秒後
重なった部分は台形で、面積はだんだん大きくなっていきます。
4秒後→18cm²
5秒後→36cm²
◎5秒後~7秒後
重なった部分は五角形で、面積はだんだん大きくなっていきます。
5秒後→36cm²
7秒後→54cm²
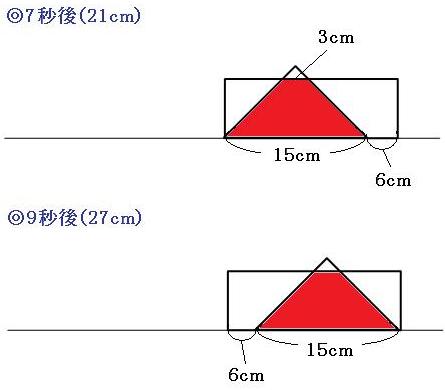
◎7秒後~9秒後
重なった部分は台形で、面積は変化しません。
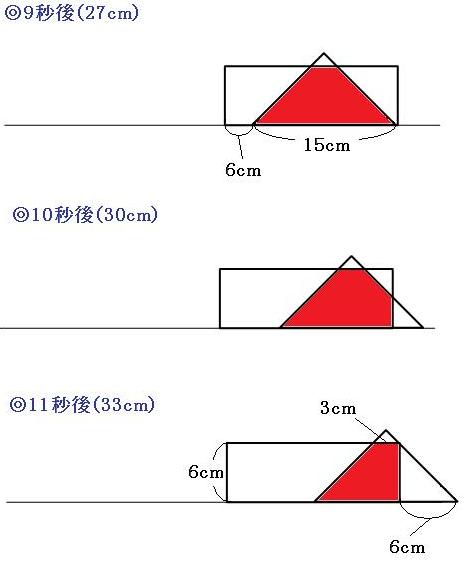
◎9秒後~11秒後
重なった部分は五角形で、面積はだんだん小さくなっていきます。
9秒後→54cm²
11秒後→36cm²
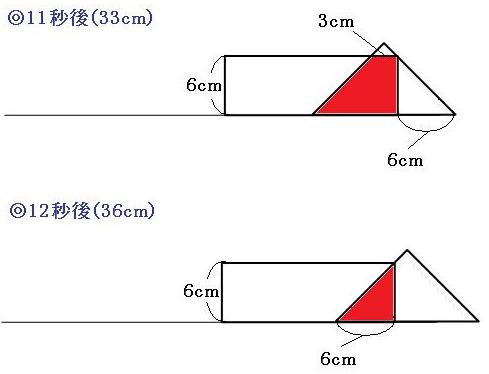
◎11秒後~12秒後
重なった部分は台形で、面積はだんだん小さくなっていきます。
11秒後→36cm²
12秒後→18cm²
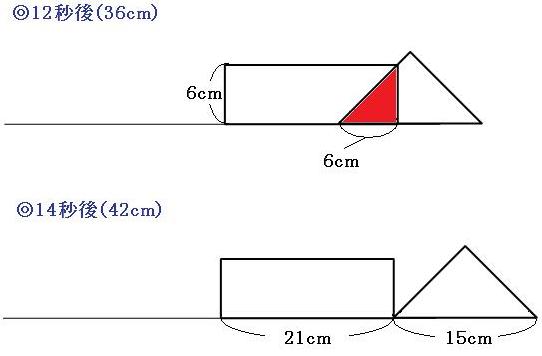
◎12秒後~14秒後
重なった部分は直角二等辺三角形で、面積はだんだん小さくなっていきます。
12秒後→18cm²
14秒後→0cm²
ということで、台形になるのは3回
4秒後から5秒後、7秒後から9秒後、11秒後から12秒後
(3)ふたつの図形が重なっている部分の面積が0.18cm²になるのは何秒後でしょう。
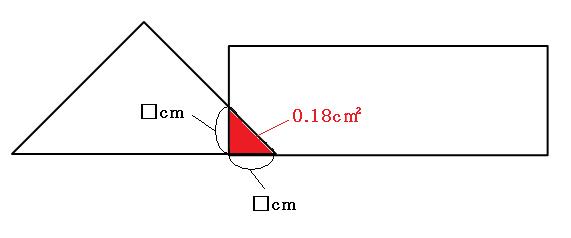
重なった部分の面積が0.18cm²になるのは、「2秒後~4秒後」の間と、「12秒後~14秒後」の2回です。どちらも形は直角二等辺三角形です。←(2)でまとめた所を参考にしてください。
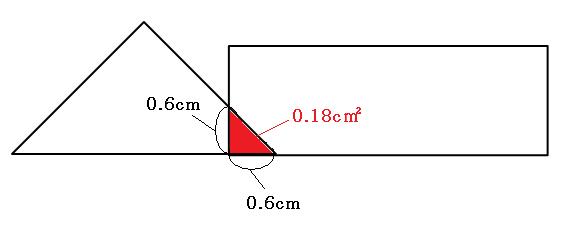
まずは、「2秒後~4秒後」の間を考えましょう。
上の図より、
□cm×□cm÷2=0.18cm²
□×□=0.36
(□や文字を求める計算の解き方)
同じ数を2回かけると0.36になるので、 □=0.6cm
これは、スタートから6.6cm進んだ状態です。移動の速さは秒速3cmでしたので、かかった時間は、
6.6cm÷秒速3cm=2.2秒
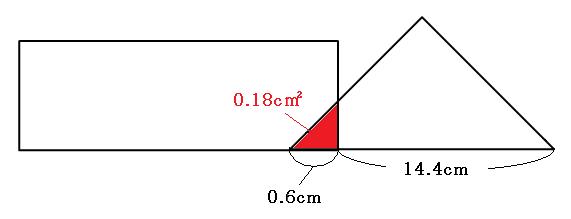
続いて、「12秒後~14秒後」の間も同じようにして、
これは、スタートから6cm+21cm+14.4cm=41.4cm進んだ状態です。かかった時間は、
41.4cm÷秒速3cm=13.8秒
よって答えは
2.2秒後、13.8秒後
(4)ふたつの図形が重なっている部分の面積が27cm²になるのは何秒後でしょう。
重なった部分の面積が27cm²になるのは、「4秒後~5秒後」の間と、「11秒後~12秒後」の2回です。どちらも形は台形です。←(2)でまとめた所を参考にしてください。
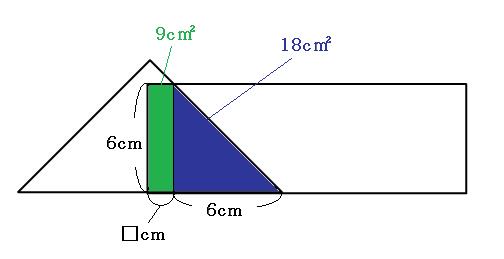
まずは、「4秒後~5秒後」の間を考えましょう。
台形のままで考えても良いのですが、直角二等辺三角形と長方形に分けた方が計算は簡単です。
上の図の青い直角二等辺三角形の面積は、
6cm×6cm÷2=18cm²
なので、緑の長方形の面積は、
27cm²-18cm²=9cm²
この緑の長方形のたての長さは6cmなので、横の長さは、
9cm²÷6cm=1.5cm
これは、スタートから6cm+7.5cm=13.5cm進んだ状態です。かかった時間は、
13.5cm÷秒速3cm=4.5秒
続いて、「11秒後~12秒後」の間も同じようにして、
これは、スタートから6cm+21cm+7.5cm=34.5cm進んだ状態です。かかった時間は、
34.5cm÷秒速3cm=11.5秒
よって答えは
4.5秒後、11.5秒後
時間とともに重なった部分がどのように変化していくかを考えてしまえば、あとは普通に図形の問題(と、ちょっぴり速さの問題も)です。
いろいろまとめて考えてしまうと、頭がこんがらがってしまうので、「今は○秒後~○秒後のお話。」と、ひとつひとつゆっくり考えてみてください。
それでは、図形の平行移動の問題をまとめます。
前のページの、図形上の点の移動とほぼ同じでした(´・ω・`)
次は、回転移動します。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!