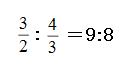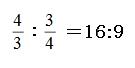歩幅と歩数

歩幅と歩数と速さの比
速さは、正式には時間と道のりを使って「時速○km」や「秒速○m」のように表されますが、工夫次第では他にもいろいろな方法で表すことができます。
例えば、「1秒間に階段を3段上がるから、秒速3段」や、「1分間に30回転するから、分速30回転」のような表し方があります。
中学受験の算数でよく使われるのは、歩幅と歩数です。速さの比と合わせてよく出題されます。
問題の文章だけ読んでも始めはチンプンカンプンだと思うので、必ず図を書いて考えましょう。
スポンサーリンク
(例題1)穂乃果(ほのか)さんが3歩で歩く距離を、海未(うみ)さんは4歩で歩きます。
穂乃果さんが4歩歩く間に、海未さんは3歩歩きます。穂乃果さんと海未さんの歩く速さの比は、何対何でしょう。
まずは、歩幅に注目して図を書いてみます。ふたりの足がそろう場所を「0、1、2」として書いておくと、あとで計算が楽になります。
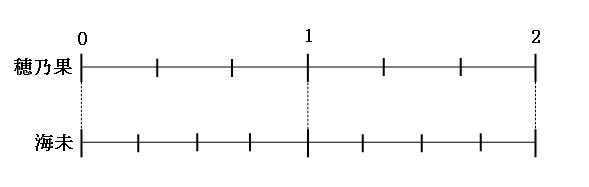
さらに、同じ時間で穂乃果さんは4歩、海未さんは3歩歩くことも図に書き加えます。
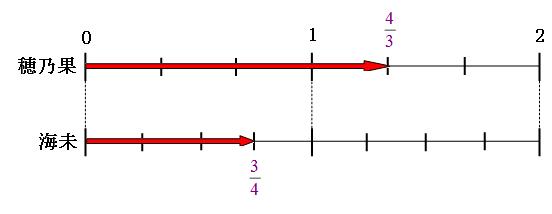
時間が同じならば、道のりの比と速さの比は同じです。(速さと比の解説はこちら)
よって、穂乃果さんと海未さんの歩く速さの比は、
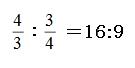
(分数の比の計算方法)
よって答えは
16:9
歩幅と歩数の問題の解き方
歩幅と歩数と速さの比は、セットにして出されることが多いです。
出題者からしてみると、1問で2つのことを問えるのでお得なのです。
なので、速さと比をしっかりと練習してからトライしましょう。
(例題2)神社の周りで、凛(りん)さんと花陽(はなよ)さんがランニングをしています。
凛さんが2歩で走る距離を、花陽さんは3歩で走ります。凛さんが3歩走る間に、花陽さんは4歩走ります。
凛さんは30分でゴールしました。。花陽さんはゴールするのに何分何秒かかるでしょう。
まずは、歩幅と歩数の図を書いて、凛さんと花陽さんの速さの比を求めます。
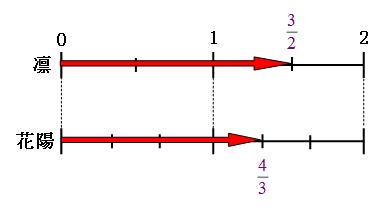
図より凛さんと花陽さんの速さの比は、
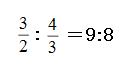
凛さんと花陽さんがゴールをするまでに走った道のりは同じです。
道のりが同じならば、速さと時間は逆比になるので、凛さんが走った時間と花陽さんが走った時間の比は8:9。
これをもとに比例式を作ると、
8:9=30分:□分
8:9=1800秒:□秒
8×□=16200
□=2025秒
(比例式の解き方)
2025秒÷60=33あまり45
よって答えは
33分45秒
歩幅と歩数の線分図が書けるようになってしまえば、もうマスターしたも同然です。
それでは、歩幅と歩数をまとめます。
ここまでで、速さと比に関する問題は終わりです。次は、図形の上を点が動くお話です。
スポンサーリンク
エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!
保護者向けの人気記事
転塾を考えるときにやるべき3つのこと
成績が上がらなければ塾を変えるべきか。塾の内部を知る講師からの目線で、失敗しない塾の選び方のコツを紹介しています。
【中学受験】スタサプの2つのデメリットを克服する方法
スタサプで成績を上げるために必要なことを解説します。
子どもが勉強したがらない!勉強のやる気アップのポイントはたった1つだけ
勉強のやる気アップのポイントを解説します。(note記事)
中学受験のための算数塾が電子書籍になりました!
超基本から難関中学過去問に挑戦できるレベルへ!20年以上塾で教えてきた著者が「速さって何だろう?」という根本から丁寧に解説をします。
塾講師・先生向けの人気記事
初心者脱却!塾講師のための12のコツ
塾講師の本質的なテクニック!20年以上塾で教えてきた著者が、塾講師として必ず知っておいてほしいコツを12個にまとめました。
【塾講師・教室長向け】三者面談を失敗させない4つのポイント
塾講師や教室長が三者面談を行う時のコツと、売上げをアップさせるために必要な事を解説します。(note記事)
【失敗回避】塾講師をするなら集団授業か個別授業か
集団授業の塾講師になるメリットとデメリット、個別授業の塾講師になるメリットとデメリットを解説します。
ブラック企業でブラックバイト塾講師を雇ってた話
私がブラック企業の個人指導塾で教室長として働いていた時に、ブラックバイト講師を雇っていた時の話をします。