容器を傾ける問題

底のふちと上のふちに水面がくるように傾けるとき
なんとか言葉で説明しようとしたのですが、こんな意味の分からないタイトルになってしまいました。「底のふちと上のふち」ってナニソレイミワカンナイ。自分で書いておきながら。
なので、絵で書きます。
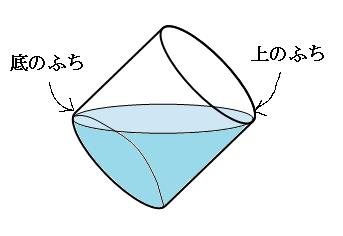
上の図のように容器を傾けると、水は満タンのちょうど半分入ります。
スポンサーリンク
(例題1)
底面の半径が6cm、高さが10cmの円柱の容器に水を入れて、上の図のように傾けます。
入っている水の体積は何cm³でしょう。
図のように傾けると、水は満タンのちょうど半分になるので、
容器の円柱の容積÷2
=6cm×6cm×3.14×10cm÷2
=565.2
よって答えは
565.2cm³
問題によっては容器が直方体の場合もありますが、同じように考えて大丈夫です。
普通に傾けるとき
先ほどのような特別な傾け方ではない場合は、真っ直ぐにした時の深さがどうなるのかを考えます。
真っ直ぐにした時の深さは、傾けていた時に一番浅かった部分と、一番深かった部分のちょうど真ん中になります。
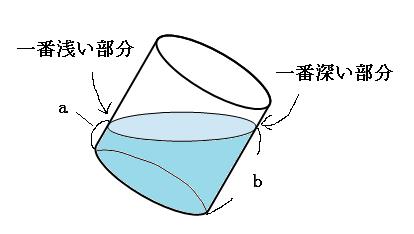
⇩真っ直ぐにすると

容器が直方体の場合、何ヶ所か深さが書いてあることがありますが、一番浅い部分と一番深い部分の2ヶ所にだけ注目すれば大丈夫です。
(例題2)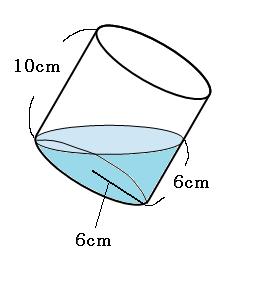
底面の半径が6cm、高さが10cmの円柱の容器に水を入れて、上の図のように傾けます。
入っている水の体積は何cm³でしょう。
一番浅い部分が深さ0cm、一番深い部分が深さ6cmなので、この容器を真っ直ぐにすると水の深さは、
(0cm+6cm)÷2=3cm
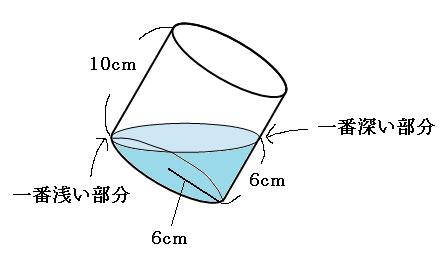
⇩真っ直ぐにすると

なので水の体積は、
底面の面積×深さ
=6cm×6cm×3.14×3cm
339.12
よって答えは
339.12cm³
(例題3)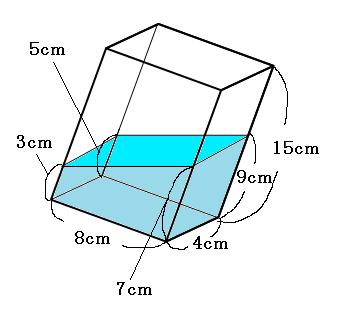
たて4cm、横8cm、高さ15cmの直方体の容器に水を入れて、上の図のように傾けます。
入っている水の体積は何cm³でしょう。
ゴチャゴチャと長さが書いてありますが、注目するのは一番浅い部分と一番深い部分だけです。
一番浅い部分が深さ3cm、一番深い部分が深さ9cmなので、この容器を真っ直ぐにすると水の深さは、
(3cm+9cm)÷2=6cm
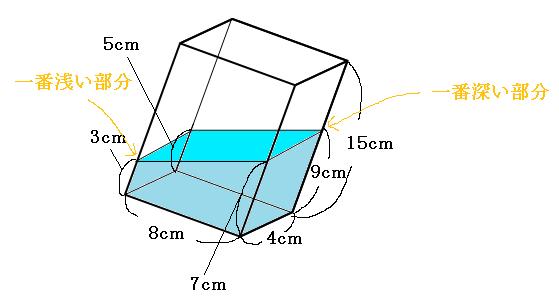
⇩真っ直ぐにすると
なので水の体積は、
底面の面積×深さ
=4cm×8cm×6cm
=192
よって答えは
192cm³
いろいろ書いてある長さにまどわされないようにしましょう。
それでは容器を傾ける問題をまとめます。
次は、水の中に立体を入れます。
スポンサーリンク
エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!
保護者向けの人気記事
転塾を考えるときにやるべき3つのこと
成績が上がらなければ塾を変えるべきか。塾の内部を知る講師からの目線で、失敗しない塾の選び方のコツを紹介しています。
【中学受験】スタサプの2つのデメリットを克服する方法
スタサプで成績を上げるために必要なことを解説します。
子どもが勉強したがらない!勉強のやる気アップのポイントはたった1つだけ
勉強のやる気アップのポイントを解説します。(note記事)
中学受験のための算数塾が電子書籍になりました!
超基本から難関中学過去問に挑戦できるレベルへ!20年以上塾で教えてきた著者が「速さって何だろう?」という根本から丁寧に解説をします。
塾講師・先生向けの人気記事
初心者脱却!塾講師のための12のコツ
塾講師の本質的なテクニック!20年以上塾で教えてきた著者が、塾講師として必ず知っておいてほしいコツを12個にまとめました。
【塾講師・教室長向け】三者面談を失敗させない4つのポイント
塾講師や教室長が三者面談を行う時のコツと、売上げをアップさせるために必要な事を解説します。(note記事)
【失敗回避】塾講師をするなら集団授業か個別授業か
集団授業の塾講師になるメリットとデメリット、個別授業の塾講師になるメリットとデメリットを解説します。
ブラック企業でブラックバイト塾講師を雇ってた話
私がブラック企業の個人指導塾で教室長として働いていた時に、ブラックバイト講師を雇っていた時の話をします。




















