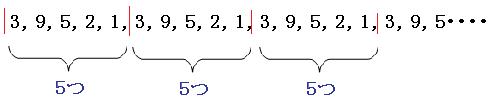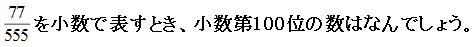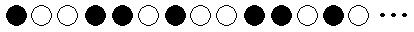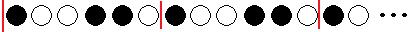規則性①　周期算

周期算とは

数字や図形、物などを規則正しく並べる規則性の問題全体を周期算と呼ぶ人もいますが、ここでは、数字や物を横一列に、規則にしたがって並べるものを周期算と呼びます。
数列も、周期算として考える人もいます。

周期算の解き方

周期算は、どんな規則で並んでいるのかを見つけられれば、もう解けたも同然です。あとは問題をよく読んで、聞かれたものを答えていきましょう。

（例題1）数字が、あるきまりにしたがって並んでいます。
3, 9, 5, 2, 1, 3, 9, 5, 2, 1, 3, 9, 5……

（1）左から128番目の数は何でしょう。

（2）左から数字を順に足していくとき、和が128を超えるのは、何番目まで足したときでしょう。

（1）左から128番目の数は何でしょう。

まずは、どんなきまりで数字が並んでいるのかを考えましょう。
同じ数字の繰り返しになっているのが見えますでしょうか。

このように、「3, 9, 5, 2, 1」の5つの数字を1セットとして並んでいます。

それでは128番目の数を考えていきましょう。まずは、128番目までに、この「3, 9, 5, 2, 1」のセットが何セットできるか求めましょう。1つのセットに5つの数字が入っているので、

128÷5＝25あまり3

よって、25セットできて、3つの数があまります。

よって答えは

（2）左から数字を順に足していくとき、和が128を超えるのは、何番目まで足したときでしょう。

1セットの中の5つの数字を足してみましょう。

3＋9＋5＋2＋1＝20

合わせて128になるまでに、この「20」のセットがいくつできるか考えます。

128÷20＝6あまり8

つまり、128になるためには6セットと、あと8必要ということになります。

なので、128を超えるのは、6セット+2番目の数「9」になります。1セットには5つの数が入っているので、この「9」が左から何番目の数なのかを考えると、

5つ×6セット+2つ＝32

よって答えは

32番目

「○セット」「○番目」「○つ」など、いろいろな数字が出てくるのでこんがらがりやすいです。数字だけでなく、「セット」「番目」などの単位をつけてノートを書き、慣れるまではゆっくりと考えながら解きましょう。

（例題2）

さっそく小数に直してみましょう。

はじめの「0.1」のところまではきまりがありませんが、その後ろは「387」のくり返しです。
ですので、小数第100位までに、この「387」のセットが、何セットできるのかを考えましょう。小数代100位までに、0でない数字は100個出てきますが、はじめの「0.1」の部分は考えないので、99個の数字が出てくると考えて、

99÷3＝33あまり0

ぴったり33セットできて、あまりはありません。