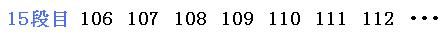規則性② 数を並べる問題
数を並べる問題とは
前のページでも数字を並べましたが、今度は真っ直ぐ横に並べるのではなく、いろいろな形に並べていきます。
四角く並べたり、段々に並べたり、ピラミッド型に並べたりします。そして、○段目の□番目の数字を求めたり、数字が何行目の何列目にあるか求めたりします。
数を並べる問題の解き方
数を並べる問題は、「一番はじっこの数字がどんなきまりで増えているか」を考えると分かりやすいです。
ちょっと言葉では説明しづらいので、例題を解きながら解説していきます。
数列や等差数列の考え方を多く使うので、必要ならば復習をしてからトライしてください。
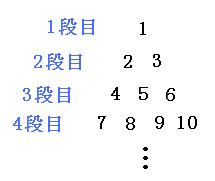
（1）111は、何段目の、左から何番目にあるでしょう。
（2）100段目の、左から32番目の数はなんでしょう。
（1）111は、何段目の、左から何番目にあるでしょう。
111くらいならば地道に書いていけば答えは求められますが、ここではもっとスマートに（かしこく）いきましょう。
それぞれの段の左はしの数字が、どんなきまりで増えていくのかを考えてみます。
このように左はしの数は、最初の「1」から、＋1、＋2、＋3と増えていきます。左はしの数字だけを求めていくと、
1段目： 1
2段目： 1＋1＝2
3段目： 1＋1＋2＝4
4段目： 1＋1＋2＋3＝7
5段目： 1＋1＋2＋3＋4＝11
6段目： 1＋1＋2＋3＋4＋5＝16
7段目： 1＋1＋2＋…＋6＝22
8段目： 1＋1＋2＋…＋7＝29
9段目： 1＋1＋2＋…＋8＝37
10段目：1＋1＋2＋…＋9＝46
11段目：1＋1＋2＋…＋10＝56
12段目：1＋1＋2＋…＋11＝67
13段目：1＋1＋2＋…＋12＝79
14段目：1＋1＋2＋…＋13＝92
15段目：1＋1＋2＋…＋14＝106
16段目：1＋1＋2＋…＋15＝121
16段目の左はしの数が111を超えてしまったので、目的の「111」は15段目にあることがわかります。
続いて、「111」が15段目の左から何番目の数なのかを考えます。15段目の左はしの数が「106」なので、ひき算をして求めるのですが、左はしの数を「1番目」と数えるので、
111－106＋1＝6
最後の「＋1」がよく分からないという人は、植木算を復習してみてください。（植木算の解説はこちら）
どうしても不安ならば、15段目だけ書き出してみるとよいと思います。
よって答えは
15段目、左から6番目
（2）100段目の、左から32番目の数はなんでしょう。
気合を入れれば100段目の左のはしの数をこのまま書き出していけますが、ここではもっとスマートに（かしこく）いきましょう。
先ほどの法則にしたがって100段目の左はしの数を考えると、
100段目：1＋1＋2＋…＋99
と、なります。最初の「1＋」の部分はダメなのですが、そのあとの「1＋2＋3＋4＋…＋98＋99」の部分は、等差数列の和の法則を使えば簡単に求めることができます。（等差数列の解説はこちら）
上の赤い四角の中の部分は等差数列で、初めの数が1、最後の数が99、項の数が99個なので、
（初めの数＋最後の数）×項の数÷2
＝（1＋99）×99÷2
＝4950
最初の「1＋」の部分も合わせて、
1＋4950＝4951
これで、100段目の左はしの数が「4951」であることがわかりました。
求める数は、この段の左から32番目の数なので、
4951＋32－1＝4982
最後の「－1」は、植木算的なアレです。
よって答えは
4982
さすがに100段目まで地道に書き上げる人はいないと思いますが、こういった問題はなるべくスマートに解くのがかっこいいです。 というか、テスト中にこんなの書き上げてるひまはありませんし。
（1）103は、何行目の何列目にあるでしょう。
（2）17行目、4列目の数はなんでしょう。
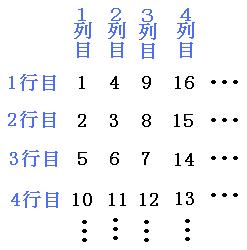
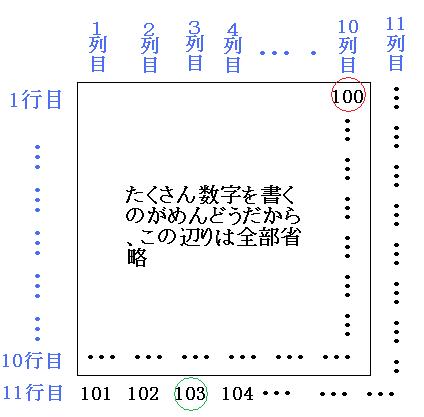
（1）103は、何行目の何列目にあるでしょう。
103くらいなら地道に書いていけば求められますが、ここではもっとスマートに（かしこく）いきましょう。
今回注目するの、それぞれの列の1行目（一番上の数字）です。
「1, 4, 9, 16, …」という並びを見てピンと来たのならば、普段からよく数字を意識できているということです。 そうです！この数字たちは、同じ数を2回かけた数字ですね。
1列目 : 1＝1×1
2列目 : 4＝2×2
3列目 : 9＝3×3
4列目 : 16＝4×4
このまま続けていくと、103に一番近い数になるのは「10×10＝100」です。
これをふまえた上で、10列目とか11行目とか、その辺りを書き出してみましょう。
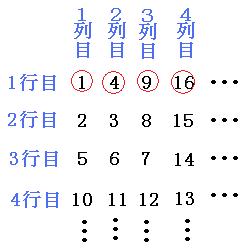
よって答えは
11行目の3列目
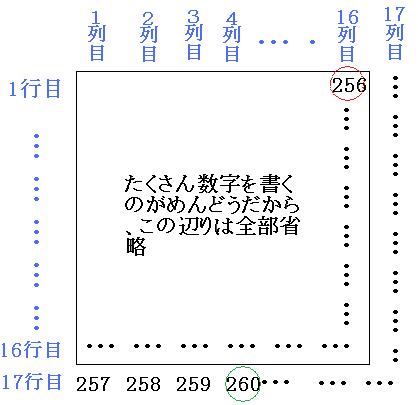
（2）17行目、4列目の数はなんでしょう。
気合いを入れれば、17行目くらいまでなら地道に書き出していけますが、ここではもっとスマートに（かしこく）いきましょう。
16列目の1行目（一番上の数字）を求めてみます。
16×16＝256
それでは、16列目とか17行目とか、その辺りを書き出してみましょう。
よって答えは
260
「1, 4, 9, 16, 25, 36, 49, …」というのは、とても大切な数字たちです。見かけたら、「あ！この子は！」って思うようになるまで頭にすり込みましょう。
ポテトチップが安売りで81円になっていたら、「あ！9×9だ！」って思うように。
前を走る車のナンバーが169だったら、「あ！13×13だ！」って思うように。
「ああ、この人は最近数字ばっかり見てておかしくなってしまったのかな・・・。」と思われるくらいに頭にすり込んでおきましょう。
それでは、数を並べる規則性の問題をまとめます。
規則性の問題はもう少し続きます。次は図形を並べます。
- 受験生応援オリジナルグッズ
エデュサポオリジナル受験生応援グッズ販売中！
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生！！
