規則性③　図形を並べる問題

図形を並べる問題

三角形や正方形などを、きまりにしたがって並べていく問題です。前のページの数字を並べる問題と同じように、四角く並べたり、段々に並べたり、ピラミッドの形に並べたりします。
図形の数だけでなく、周りの長さや面積を求めたりもします。

図形を並べる問題の解き方

「ああ！図形は苦手だよ！」っていう人も安心してください。図形問題っぽさはあまりありません。あったとしても、出題パターン少ないので、完全パターン化ができます。あくまでも規則性の問題です。
どんなきまりで並んでいるのかに注目して考えてみましょう。

（例題1）

木の棒を使って、上の図のように三角形を作っていきます。

（1）N個の三角形を作るとき、木の棒は何本必要でしょう。

（2）2000個の三角形を作るとき、木の棒は何本必要でしょう。

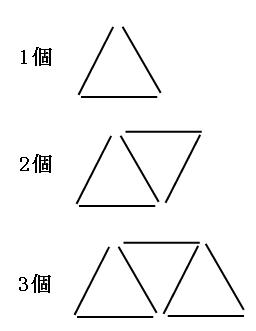
（1）N個の三角形を作るとき、木の棒は何本必要でしょう。

最初の三角形だけは木の棒が3本必要なのですが、2個目の三角形からは、木の棒は2本しか必要ありません。

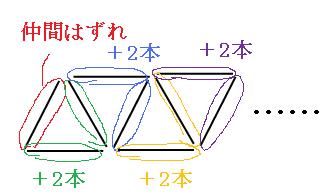
最初の三角形だけ「3本」なのがちょっと嫌ですね。規則性の問題は、なるべく単純な考え方をしたいので、ひとつだけ例外があるのは嫌がられます。では、一番左はしの一本だけ仲間はずれにしてしまいましょう。そうすれば、全て2本ずつ必要ということになります。

この考え方で、三角形を作るのに必要な木の棒の本数を書いていくと、

1個： 1＋2×1＝3本
2個： 1＋2×2＝5本
3個： 1＋2×3＝7本
4個： 1＋2×4＝9本
5個： 1＋2×5＝11本
6個： 1＋2×6＝13本
7個： 1＋2×7＝15本
N個： 1＋2×N

よって答えは

1＋2×N（本）

（2）2000個の三角形を作るとき、木の棒は何本必要でしょう。

気合いを入れれば三角形2000個くらいは書き出していけますが、ここではもっとスマートに（かしこく）いきましょう。
先ほど、N個の三角形を作るのに「1＋2×N（本）」の木の棒が必要だと分かりました。今回は2000個の三角形を作るので、Nを2000に取り替えて、

1＋2×N
＝1＋2×2000
＝4001

よって答えは

4001本

例題1の問題は、図形を並べる規則性の問題の中でも一二を争う有名問題です。ですが、かなり算数力を必要とする問題です。どれだけ理論的に考えられるかを問う、良い問題です。
なお、規則性の問題はいろいろな考え方があるので、今回の解説とは全然違う考え方で解いても問題ありません。同じ解答にたどり着いたのならば大丈夫です。
全然違う道を通ったのに答えは同じになるっていうのは、算数の面白いところだと思います。

（例題2）

1辺の長さが1cmの正方形を、上の図のようなきまりにしたがって並べていきます。

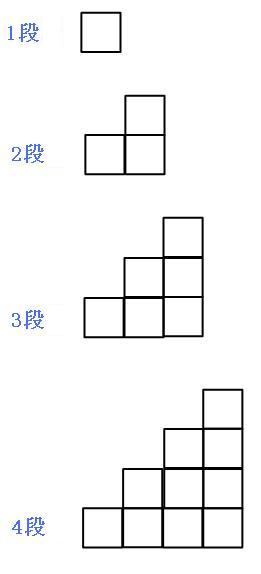
（1）100段目まで並べるとき、並べた正方形は何個になるでしょう。

（2）100段目まで並べるとき、周りの長さは何cmになるでしょう。

（1）100段目まで並べるとき、並べた正方形は何個になるでしょう。

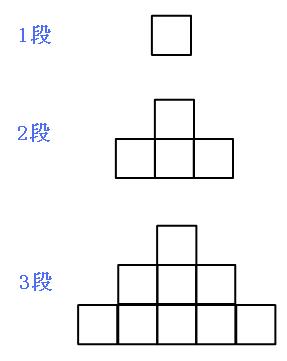
1段目は1個、2段目は「＋2個」、3段目は「＋3個」、4段目は「＋4個」…といように増えていっています。
これを並べて書いてみると、

1段目： 1
2段目： 1＋2＝3個
3段目： 1＋2＋3＝6個
4段目： 1＋2＋3＋4＝10個
5段目： 1＋2＋3＋4＋5＝15個
6段目： 1＋2＋3＋4＋5＋6＝21個
100段目： 1＋2＋3＋…＋99＋100

「1, 2, 3, 4, …, 100」というのは、初めの数が1、最後の数が100、項の数が100の等差数列です。（等差数列の解説はこちら）
その和は、

（初めの数＋最後の数）×項の数÷2
＝（1＋100）×100÷2
＝5050

よって答えは

5050個

（2）100段目まで並べるとき、周りの長さは何cmになるでしょう。

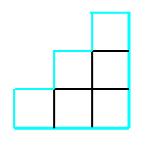
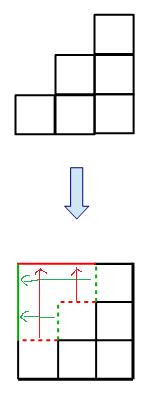
まずは、どこの長さを求めるのか確認してみます。例として、3段目の図を使ってみます。。

求める長さは、上の図の水色の部分です。このままではちょっと見づらいので工夫してみます。例として、3段の図を使ってみます。

このように段々になっている部分の辺を移動させると、1辺が3cmの正方形になりました。なので、例として使った3段目まで並べたときの周りの長さは、

3cm×4＝12cm

今回は100段目まで並べた時を考えるので、

100cm×4＝400cm

よって答えは

400cm

このように、段々になっている部分を移動させるテクニックはよく使います。とても便利ですよ！

（例題3）

正方形を上の図のようなきまりにしたがって並べていきます。100段目まで並べるとき、並べた正方形は何個になるでしょう。

正方形はどのように増えているでしょうか。はじめは1個ですが、2段目は「＋3」、3段目は「＋5」、4段目は「＋7」と増えていっています。すべて奇数ですね。この規則にしたがって、6段目まで書き出してみますね。

1段: 1個
2段: 1＋3＝4個
3段: 1＋3＋5＝9個
4段: 1＋3＋5＋7＝16個
5段: 1＋3＋5＋7＋9＝25個
6段: 1＋3＋5＋7＋9＋11＝36個

このまま考えて「100段: 1＋3＋5…＋199」と、等差数列の和を考えてもよいのですが、でもでもよく見てください。
「1, 4, 9, 16, 25, 36, …」。この数字の並びはアレですね！あの子たちです！同じ数を2回かけた数字ですね！
不思議な話なのですが、奇数を足していくと同じ数を2回かけた数字になります。

これを利用すると、100段目まで並べた時の正方形の個数は、

100×100＝10000

よって答えは

10000個

どうでしょう。「あ！この子は！」って思えましたか？（前のページ参照）
それでは、図形を並べる規則性の問題をまとめます。

まとめ

図形を並べる規則性の問題を解く時は