年齢算
年齢算とは
年齢算とは、その名の通り年齢に関する問題です。「何年後に年齢は何倍になる」や、「何年前は年齢は何倍だった」といった設定が多いです。 ものすごく当たり前ですが、1年経つと1才年をとります。そこに注目して線分図を書いていくと簡単です。 和差算や分配算のような考え方が出てくるので、そちらを練習してからのほうが簡単に解けると思います。
年齢算の種類
年齢算の出題パターンは主に2つです。
- 登場人物が2人で、「何年後に(何年前に)Aの年齢がBの年齢の○倍になるでしょう。」のように問われる
- 登場人物が3人以上で、「何年後に(何年前に)AとBの年齢の和が、Cの○倍になるでしょう。」のように問われる
例題を使って、2つのパターンの年齢算の解き方を解説していきます。
年齢算① 登場人物が2人の年齢算
年齢算は基本的には線分図を書いて解いていきます。登場人物が2人の問題を解くコツは、「何年経っても年齢の差が変わることはない」という点に注目することです。
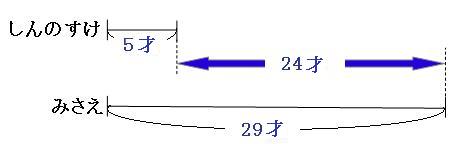
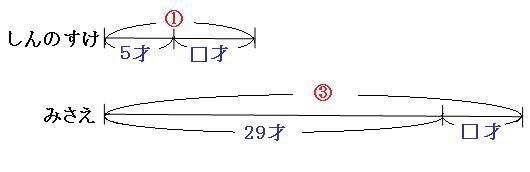
まずは、現在の線分図と、みさえの年齢がしんのすけの3倍になる□年後の線分図を書いてみます。
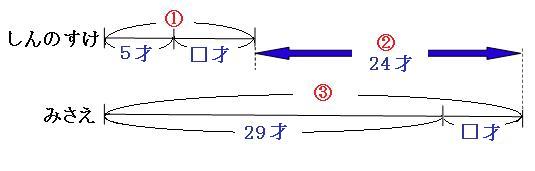
図のように、ふたりとも□才増えました。□才増えても、ふたりの年齢の差は24才のままであることに注目して、もう一度□年後の線分図を見てみます。
青い矢印の部分を見比べてみます。年齢の差はもちろん24才です。赤い丸の数字に注目すると、
③-①=②
で、②が24才にあたることがわかります。①を求めます。
24才÷②=12才
よって、①が12才にあたることがわかります。線分図を見ると、①はしんのすけの□年後の年齢なので、□年後のしんのすけは12才。 しんのすけは現在5才なので、
12才-5才=7才
よって答えは
7年後
このように、年齢の差が同じであることを意識していれば簡単です。それでは、登場人物が2人の年齢算をまとめます。
しかし、登場人物が3人以上になるともう少し工夫が必要になります。
年齢算② 登場人物が3人以上の年齢算
登場人物が3人以上になる場合、倍数算のような考え方が混ざってきます。少し応用問題になりますので、倍数算を練習してからもう一度トライしてみても良いと思います。
コツは、問題文で「年齢の和」と書かれている人物たちは1本の線分図にまとめて書き、その後で、2本の線分図の長さが同じになるように線分図を伸ばします。
文章で説明するのは難しいので、例題を使って考えていきましょう。
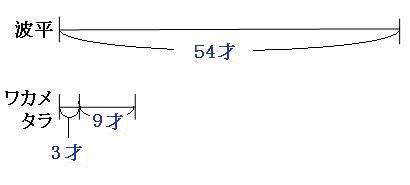
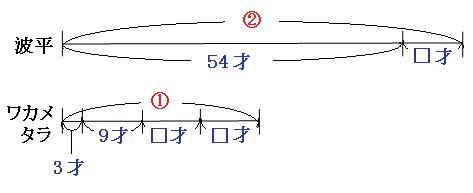
まずは、現在の線分図と、波平の年齢が、ワカメとタラちゃんの年齢の和の2倍なる□年後の線分図を書いてみます。 ワカメとタラちゃんの線分図は、1本に合体させてしまいます。
図のように、3人とも□才増えました。ワカメとタラちゃんは2人とも□才増えましたので、ワカメとタラちゃんの線分図には「□才」を2つ書きました。 登場人物が3人以上の場合は、この線分図を見ただけでは答えを求めることはできません。
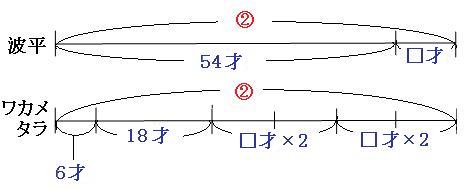
登場人物が3人以上のときは、2本の線の長さを同じにすると求めやすいです。さっそく、下の「ワカメ+タラちゃん」の線の長さをを2倍してみましょう。
線の長さを2倍にしたので、書いてある数字もすべて2倍して書きます。これで、波平の年齢の線と、ワカメ+タラちゃんの年齢の線の長さが同じになりました。この状態で、ふたつの線分図を見比べてみます。
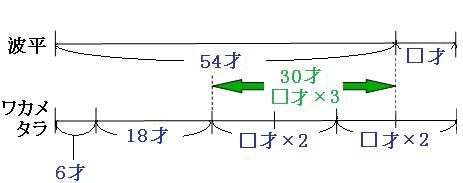
緑の矢印の部分を見比べてみます。年齢に注目して見比べると、
54才-(18才+6才)=30才
□に注目して見比べると、
□4個-□1個=□3個
よって、□が3個分で30才ということがわかります。□1個分を求めるために3で割ると、
30才÷3=10才
よって、□は1個で10才分になります。
もともと「□年後に、波平の年齢がワカメとタラちゃんの年齢の和の2倍になる」という設定をしていたので、答えは
10年後
なお、10年後は波平が64才、ワカメが19才、タラちゃんが13才ですね!
このように、3人以上登場すると手順が長くなります。「最初の線分図は書けるんだけど、線を同じ長さにするのができない。」という人は、一度「倍数算」を練習してから戻ってきましょう。
それでは、登場人物が3人以上の年齢算をまとめます。
次は相当算です。もとにする量をたくさん出します!
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!