最短距離を求める問題
図形上の最短距離
「どこを通れば距離が一番短いか。」は、普段からよく考えることだと思います。
算数でもよく問われる問題です。
「ここからここまで」みたいに2ヶ所を結ぶなら簡単です。定規で直線を引けばおしまいです。
ですが算数の問題では、「ここから、ここを通って、ここまで」のように、3ヶ所を通る場合や、「立方体の表面を、ここからここまで」のように、立体の表面を通る場合が出題されます。
平面上の最短距離
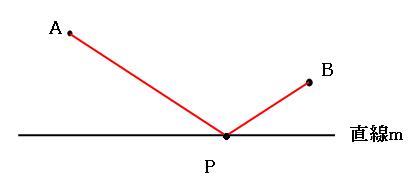
平面図形で最短距離を求める問題は、線対称の性質を利用します。
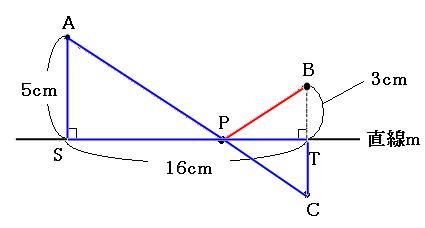
例えば上の図で、点Aから直線m上の点Pを通って点Bまで進むとします。このままでは途中で曲がってしまうのでよくわかりません。 そこで、直線mを対称の軸として、点Bに対称な点をとってみます。
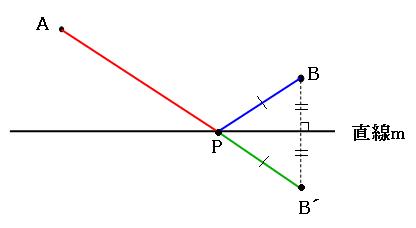
上の図の青の線と緑の線は長さが同じです。なので、実際には「赤の線+青の線」を考えなくてはいけないのですが、「赤の線+緑の線」を考えても同じことです。 これならば途中で曲がっていないので見やすいです。
さっそく、直線mを対称の軸として、点Bに対称な点をとります。
「AP+PC」が最短になれば、「AP+PB」も最短になります。
「AP+PC」が一番短くなるのは、点Aと点Cを直線で結んだ時です。なのでACは直線です。
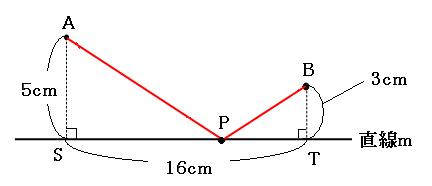
それをふまえた上で、線分SPの長さを考えます。あ!よく見るとチョウチョがいますね!!(チョウチョと相似についてはこちら)
上の図の青いチョウチョの相似比は、
AS:CT=5:3
なので、SP:TPも5:3になっています。SPの長さを求めるので、線分STを5:3に分けましょう。
![]()
よって答えは
10cm
ということで、とにかく対称な点をとって直線を引きます。
立体上の最短距離
角柱や円錐などの表面を通る線の最短距離を求める問題は、展開図を書いて考えます。 立体では分かりづらいですが、平面にしてしまえば簡単です。
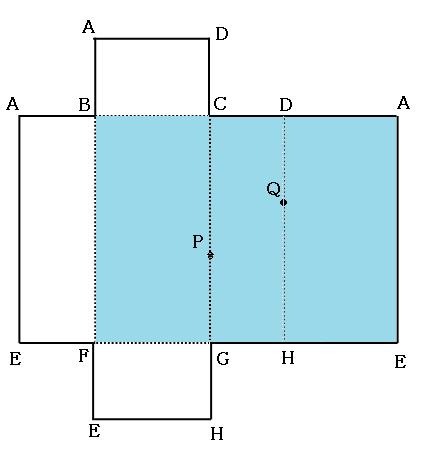
さっそく展開図を書きます。
今回は説明しやすいように、展開図全体を書きましたが、普段問題を解くときは、必要のない部分は省略してしまって構いません。
具体的には、色のついている部分だけを書けば大丈夫です。
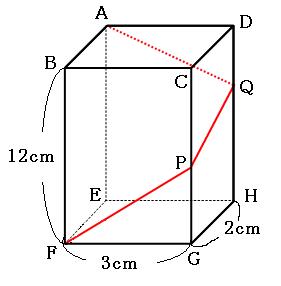
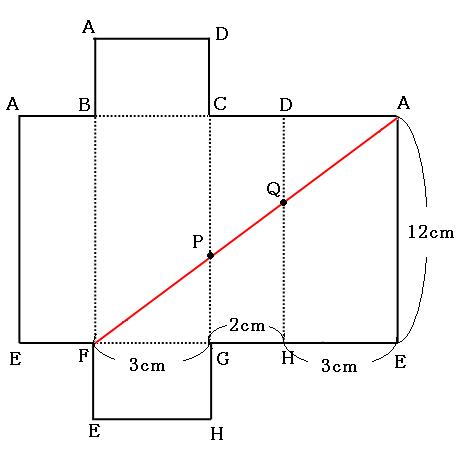
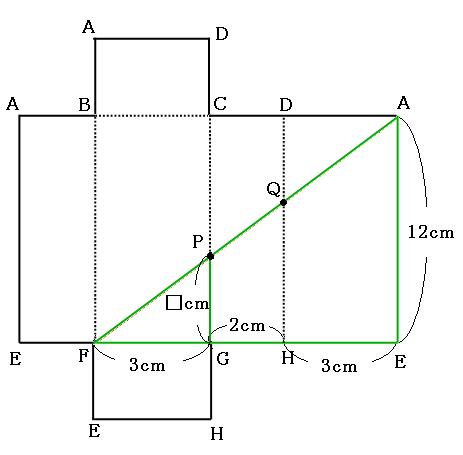
今回、点Aから、点Q、点Pを通って、点Fまでを最短距離で引くので、点A(一番右上にある点A)と点Fを直線で結ぶことになります。
さっそく定規で直線を引いてみましょう。
ここからPGの長さを求めていくのですが、トンガリがいるのが見えますでしょうか。(トンガリと相似についてはこちら)
上の図の緑のトンガリの相似比は、
FG:FE=3:8
なので、PG:AEも3:8になっています。これを使って比例式を作ると、
3:8=□cm:12cm
8×□=12×3
□=36÷8
□=4.5
(比例式の解き方)
よって答えは
4.5cm
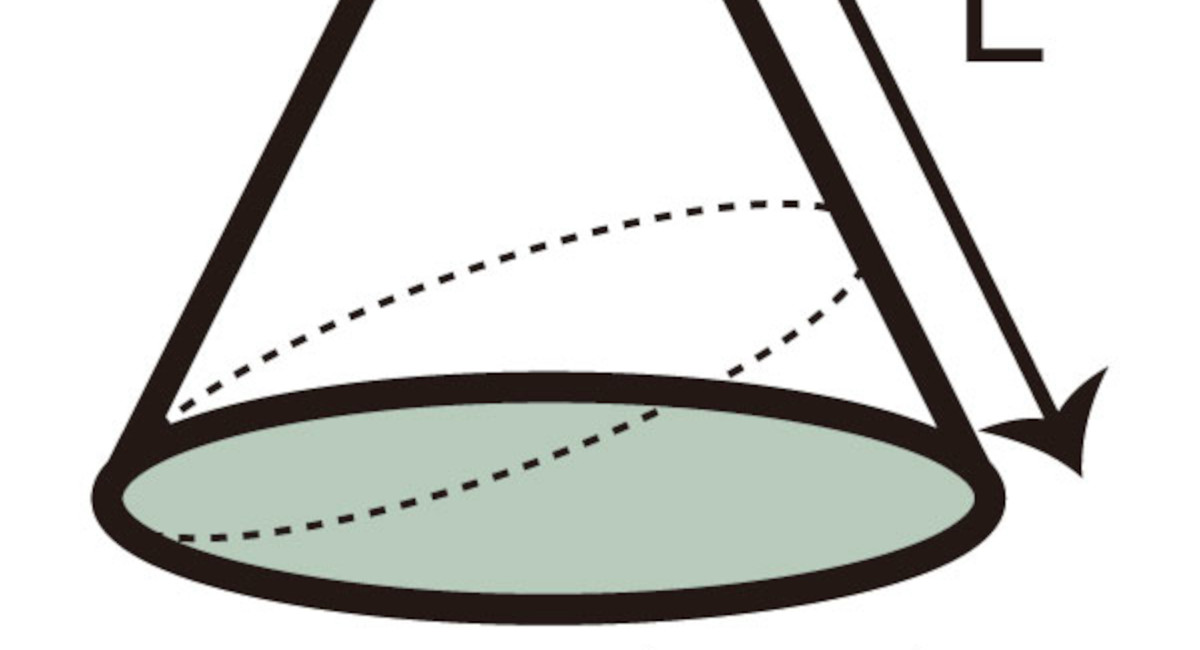
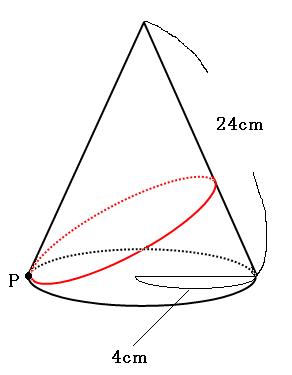
さっそく展開図を書きます。点Pから、母線にそってハサミを入れて切った図を書くとわかりやすいです。
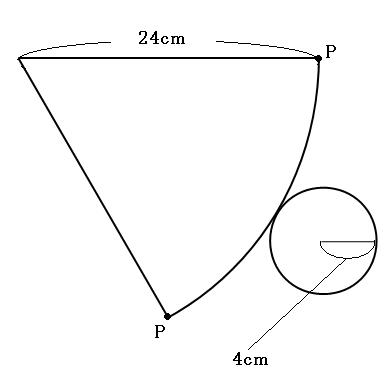
求める線分は側面を最短距離で周るので、展開図上では、左下の点Pから右上の点Pまで直線で結んだものになります。
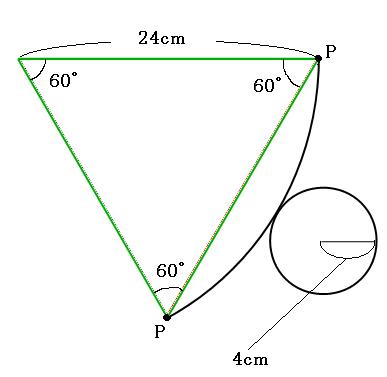
続いて、この線(上の図の赤い線)の長さを求めます。まずは、側面の展開図のおうぎ形の中心角を出してみます。(円錐の側面の展開図のおうぎ形の中心角の求め方はこちら。)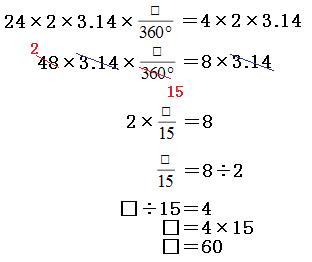
よって、中心角は60°です。さて、正三角形が見えたでしょうか?
二等辺三角形のひとつの角が60°と分かったので、他のふたつの角も60°になっています。正三角形なので、どの辺も24cmです。よって答えは
24cm
ということで、とにかく展開図を書いて直線を引きます。
それでは、最短距離を求める問題をまとめます。
次は場合の数です。「何通りあるか。」を求めていくやつです。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!