相似の問題③ 影の長さを求める相似の問題の解き方
影の長さの問題
影の長さや影の主の高さを求める問題は、相似(主にトンガリの形)を使って解きます。(トンガリについてはこちら) 相似(特にトンガリ)をマスターしてから挑戦しましょう。出題パターンは主に2つです。- 太陽の光による影
- 街灯やランプなどの光による影
太陽の光による影の長さの問題の解き方
太陽の光の問題には、必ず基準となる影の長さが書いてあります。○mの棒の影の長さが□mみたいなやつです。 それをもとにして比例式を作ってあげれば、簡単に求められます。
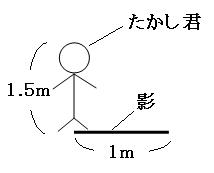
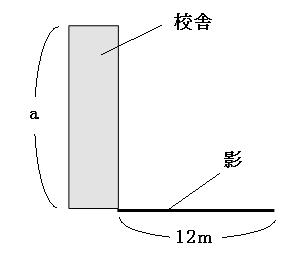
一応、たかし君の図と学校の校舎の図を書いておきます。
校舎の高さはわからないので、aと置きました。
まずは、たかし君の身長とたかし君の影の比を出しましょう。
たかし君:たかし君の影=1.5:1
=15:10
=3:2
よって、たかし君の身長とたかし君の影の比は3:2です。
同じ時刻に測ったのなら、他の物も、影の主の高さと影の長さの比は3:2になります。
つまり、学校の校舎の高さと学校の校舎の影の長さの比も3:2です。これを使って比例式を作ると。
校舎の高さ:校舎の影の長さ=
a:12m=3:2
2×a=36
a=18
(比例式の解き方)
よって答えは
18m
この方法を使えば、普段高さを測れないいろいろな物の高さを測ることができます。電柱や木や家やマンションなんかです。
基準となる比は、自分や友達の身長でもいいですし、そこら辺に落ちている棒でも構いません。
何であれ、基準となる物の高さ:その影の長さを求めて、比例式を作ればokです。
街頭やランプなどの光による影の長さの問題の解き方
街灯やランプの光でできた影の長さは、太陽の光によってできた影と違って、基準となる比を作れません。 場所や街灯の高さによって影の長さが変わってしまうからです。 ですので街頭やランプ場合、図を書いてトンガリを探します。まずは状況を図に書いてみます。
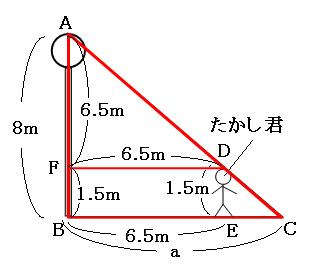
トンガリに慣れている人は、図を見た瞬間に「あ、ここにトンガリが。」って思うでしょう。 そのトンガリでも解けますが、補助線を1本引いて、別のトンガリを使ったほうが計算が楽です。
上の図の赤いトンガリの、三角形AFDと三角形ABCは相似です。相似比は、
AF:AB=6.5m:8m
=65:80
=13:16
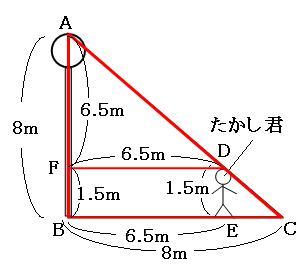
この相似比を使って、BCの長さを求めるための比例式を作ると、
13:16=6.5:a
13×a=104
a=8
よって、BCの長さは8mです。たかし君の影の長さはECの部分なので、
8m-6.5m=1.5m
よって答えは
1.5m
今回使ったトンガリでなくても構いません。好きなトンガリを使って解きましょう。
それでは影の長さの基本をまとめます。
次は、折れ曲がった影の長さを求めていきましょう。
影が折れ曲がっている
ここまでで影の長さの問題を解きましたが、どれも影は真っ直ぐでした。 ですが、影の問題では、影が途中で折れ曲がってしまっているものも多く出題されます。主な出題パターンは2つです。
- 影が壁に映っている
- 段差がある
影が壁に映っている問題の解き方
壁があるために、影が折れ曲がってしまっている問題です。 この場合、影の先から真横に補助線を引いて、トンガリを探すと求められます。(トンガリについてはこちら)
まずは図にしてみます。
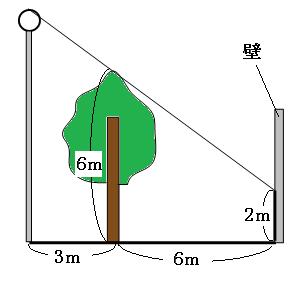
さっそく、影の先から真横に補助線を引いてみます。ついでに長さもいろいろ書き加えていきます。

図がゴチャゴチャしてしまいましたが、注目すべきトンガリを探してみましょう。
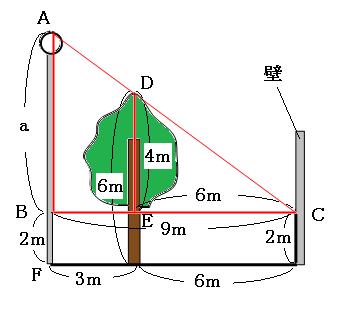
上の図の赤いトンガリは、三角形CDEと三角形CABが相似です。相似比を求めると、
CE:CB=6m:9m
=2:3
この相似比をもとに、ABの長さを求める比例式を作ると、
4m:a=2:3
2×a=12
a=6
(比例式の解き方)
よって、ABの長さは6mです。求めている街灯の高さはAFの部分なので、
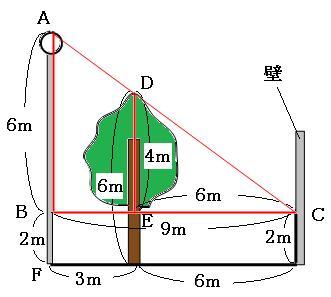
6m+2m=8m
よって答えは
8m
一番最後に2mを足し忘れてミスをすることが多いです。ここまで出せて間違えてしまったら悔しいので、最後までしっかりと気を抜かずに求めましょう。
段差がある影の問題の解き方
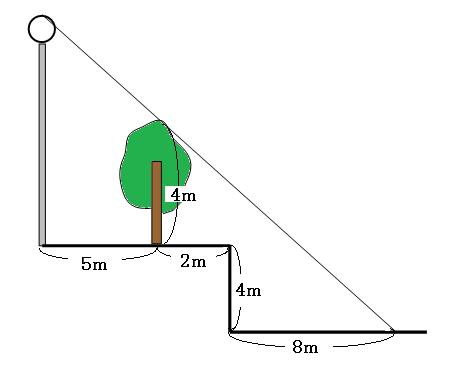
段差で影が折れ曲がってしまっている問題です。 この場合、影の先から真横に補助線を引いて、トンガリを探すと求められます。(←さっきと同じ事言ってる)
段差で影が折れ曲がってしまっています。さっそく影の先から真横に補助線を引いてみましょう。
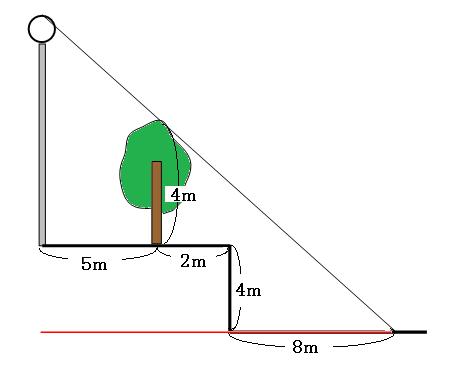
続いてトンガリを探します。
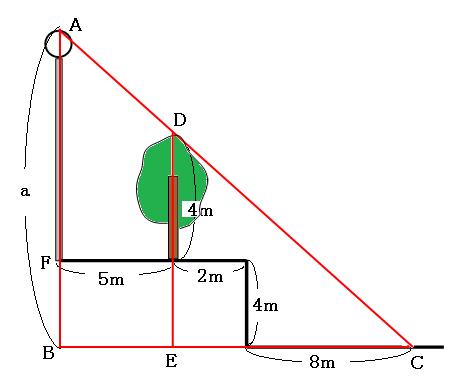
上の図の赤いトンガリは、三角形CDEと三角形CABが相似です。相似比を求めると、
CE:CB=10m:15m
=2:3
この相似比をもとに、ABの長さを求める比例式を作ると、
8m:a=2:3
2×a=24
a=12
よって、ABの長さは12mです。求めている街灯の高さはAFの部分なので、
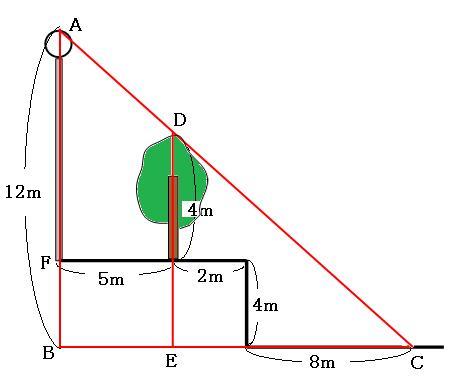
12m-4m=8m
よって答えは
8m
一番最後に4mを引き忘れてミスをすることが多いです。ここまで出せて間違えてしまったら悔しいので、最後までしっかりと気を抜かずに求めましょう。(←さっきと同じ事言ってる)
と言うことで、壁に映っていても段差になっていても、影が折れ曲がっていたら補助線を引きましょうでした。
それでは、影が折れ曲がっている問題をまとめます。
次は長さの比だけではなく、面積の比や体積の比も考えてみましょう。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!