面積図を使った食塩水の問題
食塩水の問題と面積図
食塩水の問題は、ほとんどの場合は前のページのように絵を描けば解けます。
ですが、中学受験の算数では、絵を描いただけではどうしても解けない場合があります。その場合は面積図を書いてみます。
何度か書いていますが、面積図はかけ算を使う公式とは相性がいいのです。割合には「割合×もとにする量=比べられる量」という公式があるので、面積図はとっても使えます。
食塩水の問題で面積図を使う場合、たてを濃さ、横を食塩水の重さ、面積を食塩の重さに置きかえましょう。
たて×よこ=面積
濃さ×食塩水の重さ=食塩の重さ
(割合×もとにする量=比べられる量)
この時点で「何を言っているのかわからない。」という人は、食塩水の基本を復習してから戻ってきてください。
「絵を描いても出せそうもないな。」と思ったら面積図を書くのですが、絵を描く前に、「こういう問題なら面積図」というパターンもあります。
- 食塩水の重さの合計はわかっているが、それぞれの食塩水の重さがわからないとき
- 食塩水に食塩を溶かしていて、溶かした食塩の重さを求めるとき
- 食塩水に水を混ぜていて、食塩水の重さ(または濃さ)を求めるとき
食塩水の重さの合計はわかっているが、それぞれの食塩水の重さがわからない問題の解き方
面積図の見方は、平均の問題の面積図に近いです。「こことここの面積は等しいから」というタイプの考え方です。
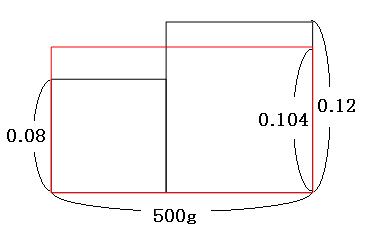
食塩水の重さの合計はわかっていますが、それぞれの食塩水の重さはわかっていません。この場合は絵を描いて考えても答えを求められないので、面積図を使って考えます。
たてを濃さ、横を食塩水の重さ、面積を食塩の重さに置きかえます。
たて×よこ=面積
濃さ×食塩水の重さ=食塩の重さ
それぞれの食塩水の重さはわからないので、横の長さは適当に書いておきます。
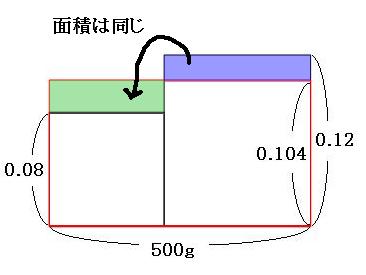
この面積図に、混ぜてできた10.4%の食塩水500gの面積図を重ねて赤で書いてみます。
混ぜる前も、混ぜた後も、食塩の重さの合計は同じなので、赤い長方形から飛び出している部分と、へこんでしまっている部分の面積は同じです。
そして、下のように面積図をわけて見てみると、
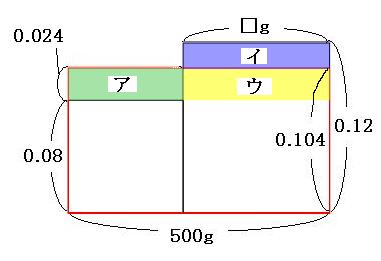
「ア」の部分と「イ」の部分の面積は同じなので、「ア+ウ」の部分と「イ+ウ」の部分の面積も同じです。「ア+ウ」の部分の面積は、
たて→0.104-0.08=0.024
横→500g
より、面積は、
0.024×500g=12g
これにより、「イ+ウ」の部分は、
たて→0.12-0.08=0.04
横→□g
面積→12g
で、あることがわかりました。なので、
□=12÷0.04=300g
これで、12%の食塩水が300gだったことがわかったので、8%の食塩水の重さは、
500g-300g=200g
よって答えは
8%…200g、12%…300g
食塩水に食塩を溶かして、溶かした食塩の重さを求める問題の解き方
食塩はすべて食塩なので、濃さ100%と考えます。
食塩水に食塩を溶かして、溶かした食塩の重さを求める問題なので、面積図を使って考えます。
たて×よこ=面積
濃さ×食塩水の重さ=食塩の重さ
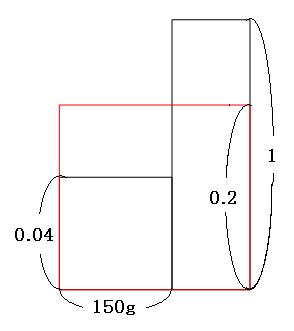
加えた食塩の重さはわからないので、横の長さは適当に書いておきます。加えた食塩は、濃さ100%として書いていきます。
例題1と同じように、赤い長方形から飛び出た部分と、へこんでいる部分の面積は同じです。
面積図より、「ア」の部分の面積は、
0.16×150g=24g
「イ」の部分の面積も24gなので、
□=24g÷0.8=30g
よって答えは
30g
食塩水に水を混ぜて、食塩水の重さ(または濃さ)を求める問題の解き方
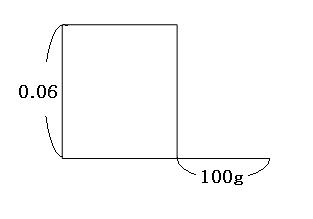
水には食塩はまったく入っていないので、濃さは0%と考えます。食塩水に水を混ぜて、食塩水の重さを求める問題なので、面積図を使って考えます。
たて×よこ=面積
濃さ×食塩水の重さ=食塩の重さ
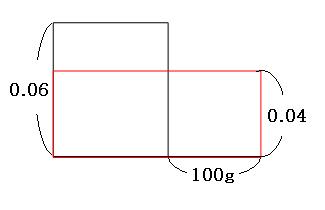
食塩水の重さはわからないので、横の長さは適当に書いておきます。加えた水は濃さ0%として、まずは6%の食塩水と、水100gの面積図を書きます。
水は濃さ0%としているので、面積図はもはやただの線です。これに、できあがった食塩水の面積図を重ねて書きます。
前の2問と同じように、赤い長方形から飛び出した部分と、へこんでいる部分の面積は同じです。
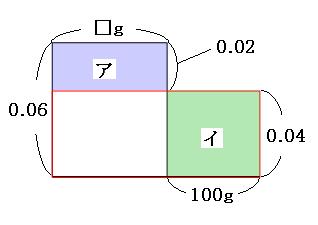
面積図より、「イ」の部分の面積は、
0.04×100g=4g
「ア」の部分の面積も4gなので、
□=4g÷0.02=200g
よって答えは
200g
食塩を加えるときも、水を加えるときも、面積図のたての長さがちょっとおかしくなってますが、スペースの都合ですすみません。
食塩を加えた時の「たての長さ1」の面積図は、本当はもっとずっとたて長ですよね。そのまま書くと、とんでもなく長い長方形になってしまうので。
それでは、面積図を使った食塩水の問題をまとめます。
面積図のお話はここまでです。次は図形です。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!