図形の周上を円が転がる問題
図形の周上を円が転がるとき
中学受験の算数では、なぜか図形の周上を円がゴロゴロと転がっていき、その円が通ったあとの面積を求めたり、中心が通ったあとの長さを求めたりします。
図形の周上を毎秒1cmで動く点よりもはるかに意味不明ですが、ボール転がしゲームだと思えばきっと楽しいです（←フォローしきれない）
直線上を転がっている間は、真っ直ぐに進むので簡単です。問題は、角の部分でどのように動くかです。
図形の外側を転がるか、内側を転がるかで変わってきます。逆に言えば、「外側を転がる」か「内側を転がる」かの2パターンしかありません。
図形の回転移動のときと同じように、おうぎ形が登場しますので、公式を載せておきます。
おうぎ形の弧の長さ
| = | 直径×円周率× | 中心角 | ||
| 360° |
おうぎ形の面積
| = | 半径×半径×円周率× | 中心角 | ||
| 360° |
円が図形の外側を転がるとき
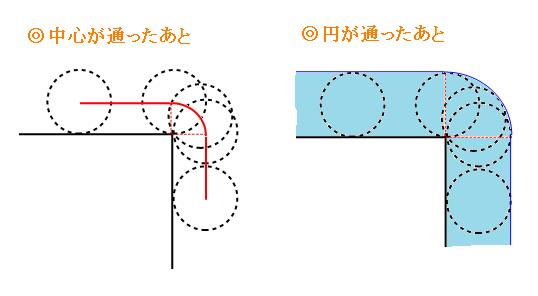
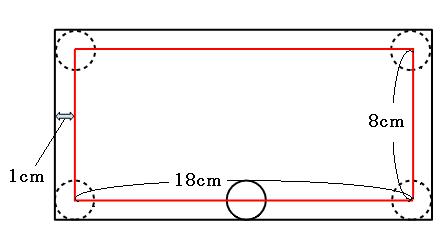
円が図形の外側を転がるとき、角の部分は、円が通ったあとも、円の中心が通ったあともおうぎ形になります。
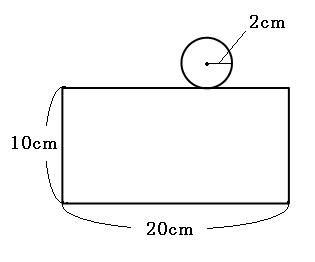
（1）円の中心が通ったあとの長さは何cmでしょう。
（2）円が通ったあとの面積は何cm²でしょう。
（1）円の中心が通ったあとの長さは何cmでしょう。
まずは、円の中心が通ったあとを書きこんでみましょう。
角のおうぎ形4つを合わせると、1つの円になります。
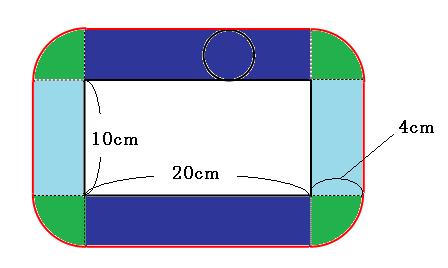
求める長さは、水色の直線部分（4本）と、緑色のおうぎ形部分（円1個分）を合わせた長さです。
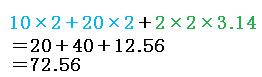
よって答えは
72.56cm
（2）円が通ったあとの面積は何cm²でしょう。
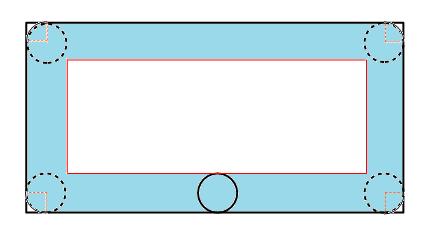
まずは、円が通ったあとを書きこんでみましょう。
角のおうぎ形4つを合わせると、1つの円になります。
求める面積は、水色の長方形（2つ）と、青色の長方形（2つ）と、緑色のおうぎ形（円1個分）を合わせた面積です。
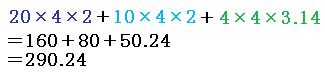
よって答えは
290.24cm²
円が図形の内側を転がるとき
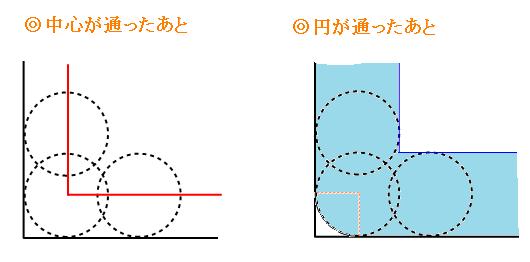
円が図形の内側を転がるとき、角の部分は、円が通ったあとの隅っこはおうぎ形に、内側はポッキリと折れ、円の中心が通ったあとはポッキリと折れます。
（1）円の中心が通ったあとの長さは何cmでしょう。
（2）円が通ったあとの面積は何cm²でしょう。
（1）円の中心が通ったあとの長さは何cmでしょう。
まずは、円の中心が通ったあとを書きこんでみましょう。
直線だけなので楽勝です。内側を回った分、長方形の辺よりも短くなっているので気をつけてください。
18×2＋8×2＝52
よって答えは
52cm
（2）円が通ったあとの面積は何cm²でしょう。
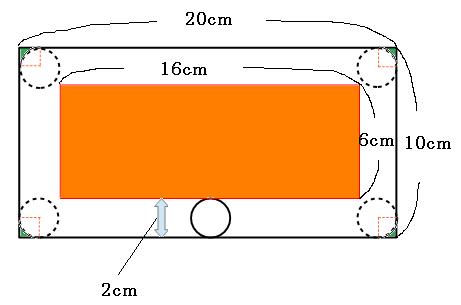
まずは、円が通ったあとを書きこんでみましょう。
この場合は、全体の面積を求めてから、いらない部分の面積を引く方法が一番楽です。
真ん中のいらない部分は長方形なので簡単に求められます。隅っこの部分を考えてみましょう。
隅っこの4ヶ所を集めて合体させてみます。
このように四隅の部分を合体させると、正方形の中に円が入っている形になります。なので、四隅のいらない部分の面積は、
2×2－1×1×3.14＝0.86cm²
求める面積は、大きな長方形から、四隅の緑色の部分と、オレンジの長方形を引いた面積です。
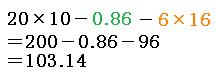
よって答えは
103.14cm²
おうぎ形の公式を使うと言っておきながら、今回は全く使いませんでしたごめんなさい。
今回は長方形の周りを転がりましたが、いろいろな図形の周りを転がることがあります。
どのような図形でも、「内側を曲がった」か「外側を曲がった」かの2パターンですので、あわてずに問いてください。
それでは、図形の周上を円が転がる問題をまとめます。
ここまでで図形の移動シリーズはおしまいです。次は表面積を求めます。
- 受験生応援オリジナルグッズ
エデュサポオリジナル受験生応援グッズ販売中！
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生！！
