旅人算の練習問題③ 応用編
旅人算の応用問題
こちらは、旅人算の応用問題を載せているページです。
旅人算の詳しい解説はこちら、基本問題はこちら、標準問題はこちらへどうぞ。
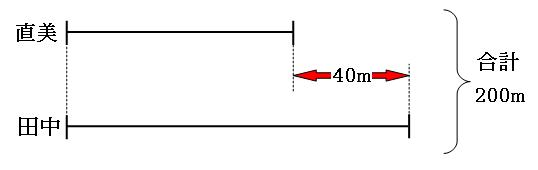
直美の速さも、田中さんの速さも分かりません。これは困りました。ですが、速さの和や差は求められそうです。
①普段の場合
普段は直美と田中さんは逆周りに回っています。9分おきにすれ違いますので、9分でふたり合わせて1800m歩くことになります。1分当たりを求めると、
1800m÷9分=200m
つまり、1分間に歩くふたりの道のりの和は200mです。
②今日の場合
今日は直美と田中さんは同じ方向に回っています。直美は45分で周回遅れにされますので、45分間で田中さんの方が1800m多く歩いたことになります。1分当たりを求めると、
1800m÷45分=40m
つまり、1分間に歩くふたりの道のりの差は40mです。
③和と差が分かりましたね!
2つの数の和と差が両方分かっている時は、迷わず和差算を使いましょう!
(和差算の解説はこちらへ)
さっそく線分図を書きます。
田中さんの線分図を求めると、
(200+40)÷2=120
なので、田中さんが1分間に歩く道のりは120m。直美が1分間に歩く道のりは、
120m-40m=80m
よって答えは
直美…分速80m
田中さん…分速120m
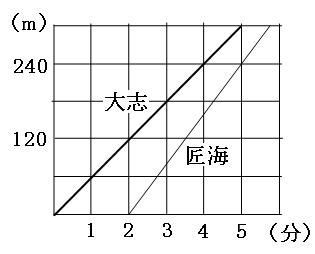
(1)匠海が大志に追いつくのは、匠海が出発してから何分後でしょう。また、それは出発地点から何mの地点でしょう。
(2)匠海と大志が進んだ道のりの和が890mになるのは、大志が出発してから何分何秒後でしょう。
(3)匠海と大志の間の道のりが12mになるのは、大志が出発してから何分何秒後でしょう。
(1)匠海が大志に追いつくのは、匠海が出発してから何分後でしょう。また、それは出発地点から何mの地点でしょう。
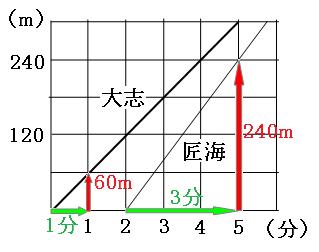
グラフを見て、2人のそれぞれの速さを求めましょう。 大志は1分間で60m、匠海は3分間で240m進んでいるのが分かります。
大志
60m÷1分=分速60m
匠海
240m÷3分=分速80m
2人は同じ方向に進んでいます
匠海が出発するまでに、大志はすでに2分歩いています。その間に歩いた道のりは、
分速60m×2分=120m
で、この時の2人の間の道のりは120mだと分かりました。、大志は1分間に60m、匠海は1分間に80m進むので、匠海が追いつくまでにかかる時間は、
120m÷(80m-60m)
=6
6分間に匠海が歩いた道のりは、
分速80m×6分=480mよって答えは
6分後、480m
(2)匠海と大志が進んだ道のりの和が890mになるのは、大志が出発してから何分何秒後でしょう。
匠海が出発するまでに、大志はすでに120m進んでいます。この部分を引いておくと、
890m-120m=770m
になるので、2人で合わせて770m進めばよいことが分かります。
大志は1分間に60m、匠海は1分間に80m進むので、合わせて770m進むのにかかる時間は、
770m÷(60m+80m)=5.5
5.5分、つまり5分30秒かかることが分かりました。大志が1人で進んだ2分もプラスして、
2分+5分30秒=7分30秒
よって答えは
7分30秒
(3)匠海と大志の間の道のりが12mになるのは、大志が出発してから何分何秒後でしょう。
2人の間の道のりが12mになるのは、3回あります。 ①匠海が出発する前と、②匠海が大志に追いつく前と、③匠海が大志を追いこした後です。
①匠海が出発する前
単純に、大志が12m進んだ時を考えましょう。
12m÷分速60m=0.2分
0.2分×60=12秒
よって12秒後
②匠海が大志に追いつく前
匠海が出発した時点で、2人の間の道のりは120mでした。2人の間が12mになる時を求めるので、あと、
120m-12m=108m
108m追いつかなければなりません。それにかかる時間は、
108m÷(80m-60m)=5.4
5.4分、つまり5分24秒です。大志が1人で歩いた2分もプラスして、
2分+5分24秒=7分24秒
よって、7分24秒後
③匠海が大志を追いこした後
匠海が大志に追いつくのは、大志が出発してから8分後です。その後、さらに12m引きはなします。
大志は1分間に60m、匠海は1分間に80m進むので、1分間で20mづつ引きはなしていくのが分かります。よって、12m引きはなすのにかかる時間は、
12m÷20m=0.6
0.6分、つまり36秒です。追いつくまでの8分もプラスして、
8分+36秒=8分36秒
よって、8分36秒後
よって答えは
12秒後、7分24秒後、8分36秒後
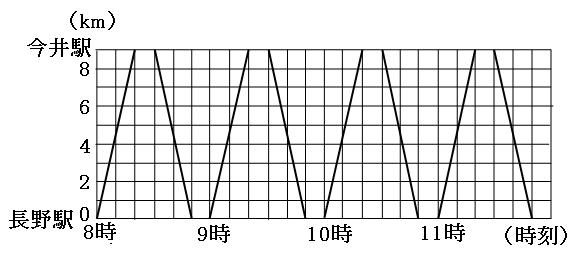
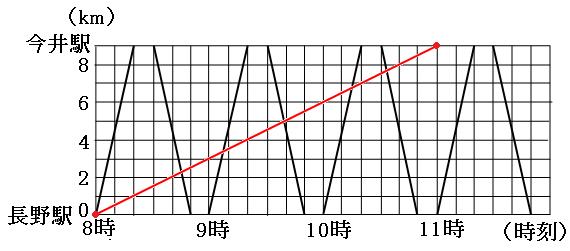
(1)一夫は、今井駅に着くまでに何回バスとすれ違ったでしょう。
(2)一夫が2回目にバスとすれ違ったのは、何時何分でしょう。
(1)一夫は、今井駅に着くまでに何回バスとすれ違ったでしょう。
一夫のグラフを書き加えます。一夫の速さは時速3kmなので、今井駅に着くまでにかかる時間は、
9km÷時速3km=3時間
つまり、11時ぴったりに今井駅についたことになります。なので、8時ちょうどに長野駅の点と、11時ちょうどに今井駅の点を定規で結ぶと、
赤い線が一夫のグラフです。今井駅から長野駅に向かっているバスと、3回すれ違っているのが見えます。
よって答えは
3回
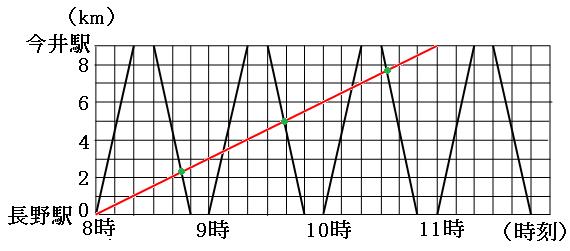
(2)一夫が2回目にバスとすれ違ったのは、何時何分でしょう。
先ほどのグラフの、2つ目の緑の点の時間を求めることになります。
まずは、バスの速さを求めておきましょう。バスは20分で9km進んでいるので、
| 20分 | = | 1 | 時間 | ||
| 3 |
| 9km÷ | 1 | 時間= | 時速27km | |
| 3 |
次に、バスが今井駅を出発する9時30分の状況を考えてみましょう。バスは今井駅にいます。一夫は出発してから1時間30分歩いていますので、その間に歩いた道のりは、
時速3km×1.5時間=4.5km
状況を図にしておくと、
あとは旅人算の考え方で解きましょう。
4.5km÷(27km+3km)
=4.5÷30
=0.15
0.15時間=0.15×60分
=9分
よって答えは
9時39分
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!