体積
○柱
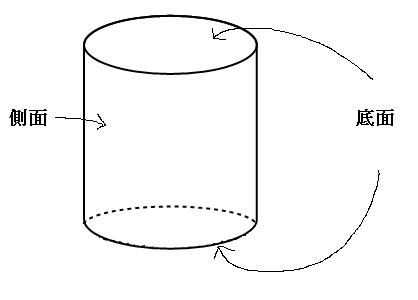
柱のように真っ直ぐ立っているような立体を「柱(ちゅう)」と呼びます。
図のように、柱の上の面と下の面を底面、横の面を側面と呼びます。
底面の形によって立体の名前が変わります。上の図は底面が円なので円柱、底面が三角形だったら三角柱、底面が五角形だったら五角柱、底面が百八角形だったら百八角柱と呼ばれます。
○錐
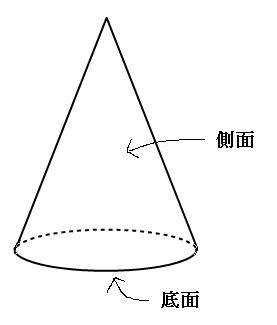
先のとがった立体を「錐(すい)」と呼びます。
図のように、下の面を底面、横の面を側面と呼びます。
こちらも底面の形によって立体の名前が変わります。上の図は底面が円なので円錐、底面が三角形だったら三角錐、底面が五角形だったら五角錐、底面が百八角形だったら百八角錐と呼ばれます。
柱と錐の体積
どちらも公式は簡単です。
柱の体積=底面の面積×高さ
錐の体積=底面の面積×高さ÷3
錐の高さは、頂点から底面に垂直に引いた線です。真っ直ぐの線です。斜めの線ではないので気をつけましょう。
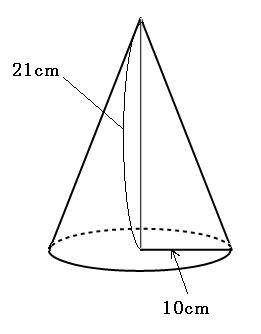
図は円錐です。底面の形は円なので、
円錐の体積=底面の面積×高さ÷3
=円の面積×高さ÷3
=10cm×10cm×3.14×21cm÷3
=2198
よって答えは
2198cm³
錐の公式一発でした。
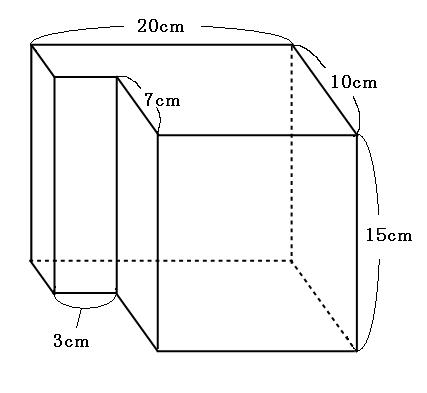
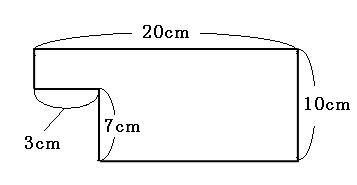
図は角柱です。まず、底面の面積を求めましょう。
底面は上の図のようになっています。自分のやりやすい方法で面積を求めてください。
20cm×10cm-3cm×7cm=179cm²
なので体積は、
底面の面積×高さ
=179cm²×15cm
=2685
よって答えは
2685cm³
必ずしも底面が上や下に書いてあるとは限りません。斜めになっていたり、ゴロンと横に転がってたりすることもあります。
どんな形で出てきても気がつくように、問題を解きながら、いろいろな図形に出会いましょう。
それでは体積をまとめます。
次は、体積と比を組み合わせます。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!