図形上の点の移動
図形上を点が移動するとき
図形上を点が移動する問題を解く時に最も大事なことは、状況をしっかりと理解し、点が動いていく様子を頭の中で想像することです。
そのためにまず、問題文をしっかりと読みましょう。どの点がどこからスタートし、どこを通って、どこまで動くのか。動く速さはどれくらいか。しっかりと読み取っておきましょう。
それを元に頭の中で点を動かせれば、問題はほぼ解けたも同然です。
あとは、問題の求めるものを出していけば大丈夫です。
「図形の上を毎秒1cmで移動する点とか、意味がわからない。」と、なにかとバカにされる問題ですが、回転寿司だと思えば美味しいので頑張ってください。
なお、私は断然イクラ派です。
図形上の点の移動の問題の解き方
基本的には、点の移動の様子を頭の中で想像するだけなのですが、どうしてもそれが苦手なようなら、いくつか実際に紙に書いてみるといいと思います。 適当に、「2秒後」「5秒後」「8秒後」などの図を書いてみると想像しやすくなると思います。
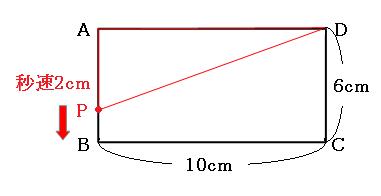
まずは問題をしかりと読んで状況を把握し、点が動いていくにしたがって、三角形APDの形がどんなふうに変わっていくか、頭の中で想像してみましょう。
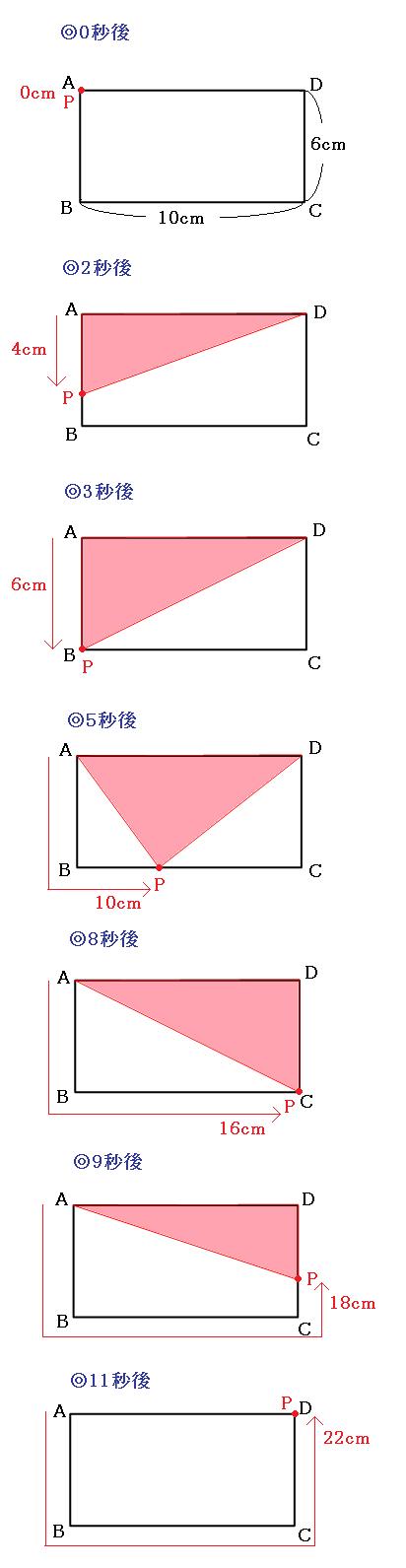
想像するのが難しいようならば、いくつか図形を書いてみます。今回は、点Pが出発してから0秒後、2秒後、3秒後、5秒後、8秒後、9秒後、11秒後を書いてみようと思います。
図を見ながら、三角形APDの面積がどのように変化していったかを見てみましょう。
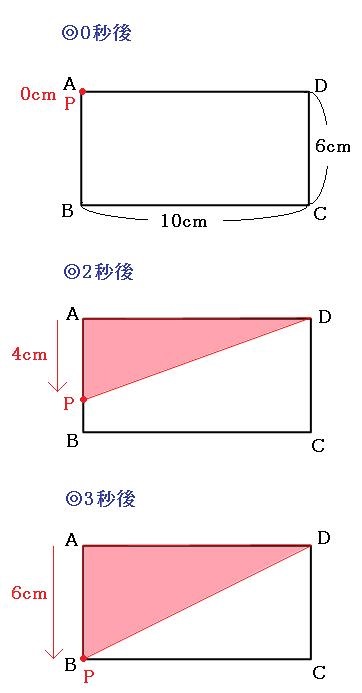
◎0秒後~3秒後
0秒の時点では面積は0です。これがだんだん大きくなっていき、3秒後に一番大きくなります。
この時の面積は、
10cm×6cm÷2=30cm²
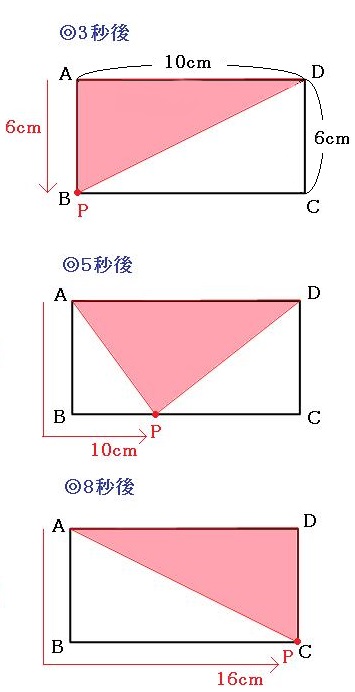
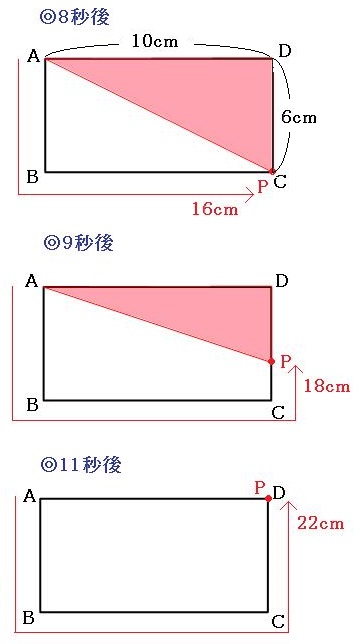
◎3秒後~8秒後
この間はずっと、底辺の長さが10cm、高さ6cmのまま変わらないので、面積は30cm²のまま変化しない。
◎8秒後~11秒後
面積は30cm²からだんだん小さくなり、11秒後には0になる。
この変化を把握できれば、問題自体は簡単です。
面積が25cm²になるのは、「0秒後~3秒後」の間に1回、「8秒後~11秒後」に1回、全部で2回あります。
辺AD(10cm)を底辺としたときの、面積が25cm²になる時の高さを求めます。
10cm×□÷2=25
5×□=25
□=5
(□や文字を求める計算の解き方)
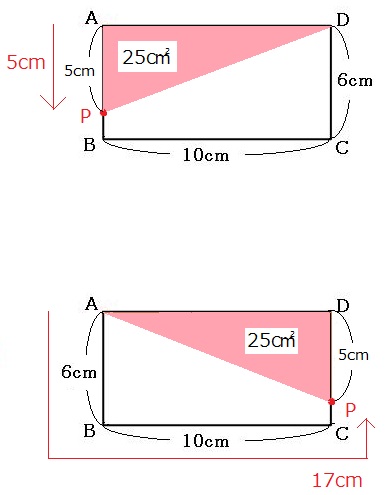
高さが5cmになるのは、点Pがスタートから5cm進んだところと、17cm進んだところです。
点Pの速さは秒速2cmなので、それぞれにかかる時間は、
◎5cmのとき
5cm÷秒速2cm=2.5秒
◎17cmのとき
17cm÷毎秒2cm=8.5秒
よって答えは
2.5秒後と8.5秒後
図を書いたりしたので解説が長くなりましたが、問題を解くときはほとんどを頭の中で想像してしまうので、それほどノートがゴチャゴチャとすることはないと思います。安心してください。
状況をノートにメモするのならば、節目となる場所の時間と面積をメモしておくと整理しやすいとおもいます。
今回の問題ならば、点Pがスタートしたとき(0秒後、0cm²)、頂点Bに着いたとき(3秒後、30cm²)、頂点Cに着いたとき(8秒後、30cm²)、頂点Dに着いたとき(11秒後、0cm²)の4ヶ所です。
複数の点が移動する問題の解き方
動く点が2個になったり3個になったりすることもありますが、基本的にはやることは同じです。状況を把握して、移動の様子を頭の中で想像します。
ただ、さすがに2個以上の点の移動を頭の中で想像するのは難しいので、節目になるシーンを図に書きながら解くのが現実的です。
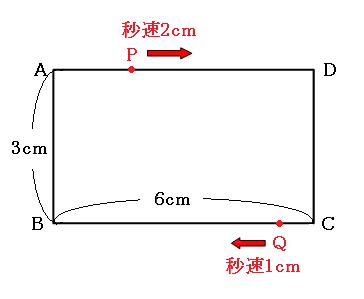
(1)四角形ABQPが最初に長方形になるのは、ふたつの点が出発してから何秒後でしょう。
(2)四角形ABQPが3回目に長方形になるのは、2つの点が出発してから何秒後でしょう。
(1)四角形ABQPが最初に長方形になるのは、ふたつの点が出発してから何秒後でしょう。
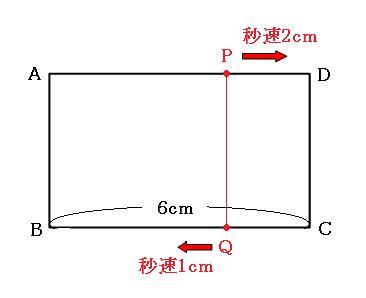
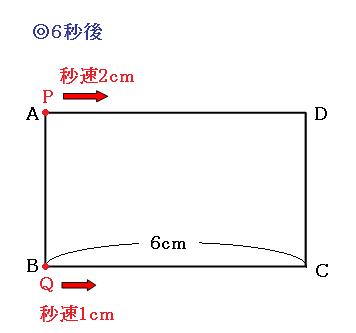
まずは、最初に四角形ABQPが長方形になるときがどんなときなのかを考えます。
上の図のようになったときが、最初に長方形になるときです。これって、あれに似てますよね。逆向きに進んで出会う旅人算に。
ということで、旅人算の解き方を使いましょう。(旅人算の解き方はこちら)
点Pが1秒間に進む道のりは2cm、点Qが1秒間に進む道のりは1cmです、
6cm÷(2cm+1cm)=2
よって答えは
2秒後
(2)四角形ABQPが3回目に長方形になるのは、2つの点が出発してから何秒後でしょう。
このあとは節目となる瞬間を図に書きながら考えていきます。
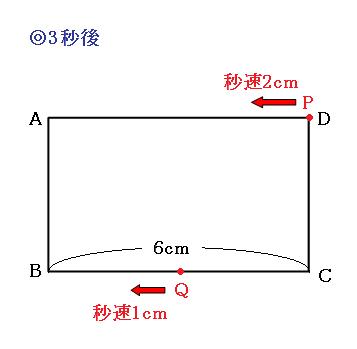
最初に節目となるのは、3秒後(点Pが頂点Dに到着するとき)です。
次は6秒後(点Pが頂点Aに到着、点Qが頂点Bに到着するとき)です。
このときはいい感じの位置になるのですが、そもそも四角形ABQPができないのでダメです。
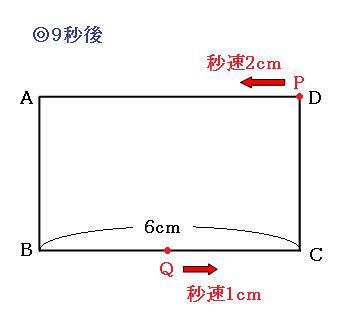
次は、9秒後(点Pが頂点Dに到着するとき)です。
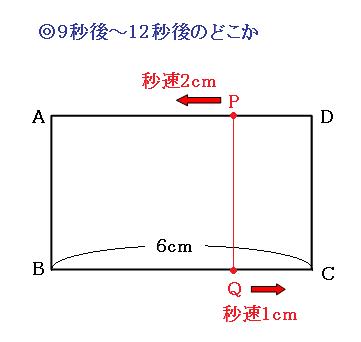
次は9秒後~12秒後のどこか(2回目の長方形ABQPができる)ときです。
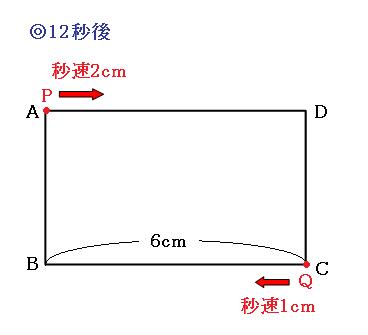
2回目の時間は聞かれていないので求めません。「この辺りで長方形ができたな。」って思うだけで大丈夫です。次は12秒後(点Pが頂点Aに到着、点Qが頂点Cに到着するとき)です。
さあ!次にすれ違うときが3回めの長方形ですよ!!
ということで、この瞬間(12秒後)から旅人算をします!
6cm÷(2cm+1cm)=2
12秒+2秒=14秒
よって答えは
14秒後
地道な作業となりました。点の移動は、こういう地道な単純作業のことが多かったりします。頑張ってください。
それでは、図形上の点の移動をまとめます。
次は図形を動かします。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!