等差数列

等差数列とは

等差数列とは、前のページで書いたように、次の項へ、同じ数を足していく数列のことです。同じ数を引いていくこともあります。

例1） 1,4,7,10,13,16,…

例2） 130,125,120,115,110,…

中学受験の等差数列では、「第○項はいくつですか？」や、「第○項までの和はいくつですか？」と聞かれます。 解説では、なぜがNを使って「第N項」などと表されることが多いです。

等差数列の第N項はいくつ？

等差数列ならば、第10項や第20項くらいまでなら地道に数えられるでしょう。が、第250項を求めなさいなんて言われたらお手上げです。 なので、計算で出せるようにしておきましょう。例として、初めの項が2、公差が3の等差数列を考えてみましょう。

2,5,8,11,14,17,20,…

例えば第3項の数は、初めの数2に3を2回足せばいいことがわかります。

2+3+3=8

同じように考えれば、第5項の数は、初めの数2に3を4回足せばいいことがわかります。

2+3+3+3+3=14

並べて書いてみると、

第1項：2
第2項：2+3=5
第3項：2+3+3=8
第4項：2+3+3+3=11
第5項：2+3+3+3+3=14
第6項：2+3+3+3+3+3=17

かけ算を使って書きかえると、

第1項：2
第2項：2+3=5
第3項：2+3×2=8
第4項：2+3×3=11
第5項：2+3×4=14
第6項：2+3×5=17

つまり、初めの数に公差を何回か足せばよいのです。公差を何回足すかなのですが、第2項で1回、第3項で2回、第4項で3回、第5項で4回と、項の数より1少ないのがわかります。 以上をまとめて、等差数列の第N項の数を求める式を考えると

第N項=初めの数+公差×(N-1)

「400項や500項くらいなら数え上げてやるぜ！」って人は頑張ってください！

等差数列の第N項までの和

こちらは足し算の答えを出すことになるので、数字も大きくなりがちで、第20項まででも足していくのはつらいと思います。 なので、しっかりと算数的に考えましょう。例として、初めの項が2、公差が3の等差数列を、第1項から第10項まで足してみましょう。

2+5+8+…+23+26+29

これくらいならば気合いで計算できそうですが、以下のように考えると簡単に出せます。

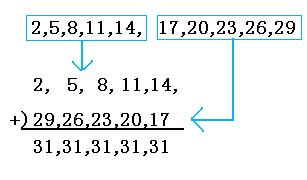
このように、数列をちょうど真ん中でぶった切って図のように並べかえて足すと、同じ数字がいくつか出てきます。今回の31という数字は、この数列の初めの数と最後の数の和になっています。 もちろん第2項と第9項の和でもあるし、第3項と第8項の和でもあるのですが、初めの数と最後の数と考えた方が簡単なので、この組み合わせで考えています。
続いて、この31を何回足すかですが、全部で10項あるものを半分にぶった切ったので、10の半分の5回と考えます。
よって、この例の等差数列の和は、

(2+29)×10÷2=155

同じように考えて第N項までの和を考えると、

第N項までの和=（初めの数+最後の数）×N÷2

こちらも、地道に計算したいという方は頑張ってください！
毎回、考え方にしたがって公式を求めてもよいですが、よく使う公式なので暗記してしまいましょう。 ただ、応用問題でも対応できるように、公式の求め方もしっかりと理解しておいてください。それでは等差数列をまとめます。

まとめ

等差数列を解くときは

1. 第N項=初めの数+公差×(N-1)
2. 第N項までの和=（初めの数+最後の数）×N÷2

の、公式を使う。

すみません、まとめと言いながら公式を書いただけです。次は木を植えます。

• 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中！

エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生！！

保護者向けの人気記事

塾講師・先生向けの人気記事

<<数列　　植木算>>

数列の練習問題へ

数列の最初のページへ

目次へ

中学受験のための算数塾TOPページへ

　

サイト内のページはすべてリンクフリーです。リンクの確認やご報告等は必要ありません。みなさまのリンクを歓迎いたします。
なお、トップページ以外のアドレスは変わる可能性がありますので、予めご了承ください。