通過算の解き方
通過算とは
通過算とは、列車や車がある地点を通り過ぎたり、鉄橋やトンネルを通ったりする際の速さ、時間、道のり等を求める問題です。問題では列車が使われることが多いです。主な出題のパターンは3種類です。
- 自分の前、またはある地点を通過する。
- 鉄橋、またはトンネルを通過する
- 列車と列車がすれ違う、または列車が列車を追い越す
通過算の解き方
どのパターンも、基本的には速さの計算問題の解き方で解けます。ただし、道のりがわかりにくいものが多いです。逆に言えば、道のりさえしっかり見えていれば、通過算はマスターしたも同然です。
その道のりを見えるようにするためのコツはただ一つ、絵を描いてみることです。
どんなに下手くそな絵でも構いません。このサイトにときどき(ひんぱんに!)出てくるような素晴らしい絵を描く必要はありませんので、とにかく描いてみてください。
ということで、通過算はお絵かきを楽しみましょう!
それでは、実際に通過算を解いてみましょう。
通過算① 自分の前またはある地点を通過する通過算の解き方
先ほど書いたように、コツはただひとつ「絵を描くこと」です。
速さの問題なので、とりあえず「みはじ」の図をどこかに書いておきましょう。
まずは状況を整理します。
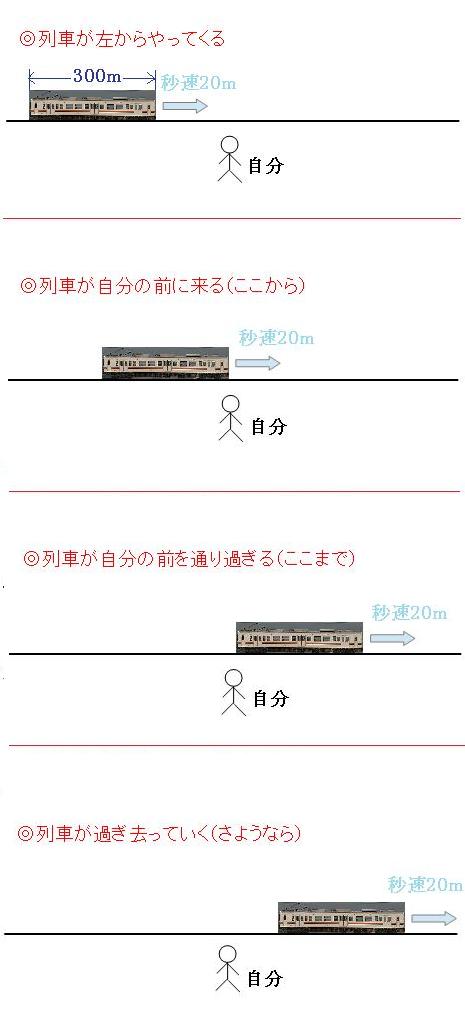
列車が左からやってきて、右に通り過ぎて行くまでの順を追うと図のようになります。それでは、列車の先頭が自分の前に来た瞬間から、列車の最後尾が自分の前を通り過ぎて行く瞬間までに列車が走った道のりを、図を使って見てみましょう。
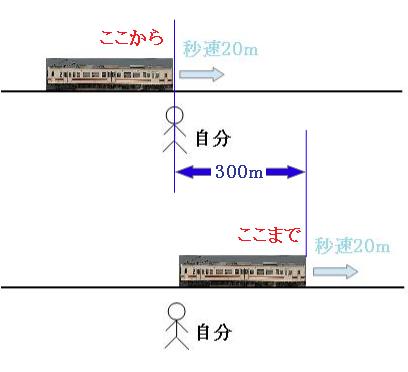
図のように、列車が自分の前を通り過ぎるのに走った道のりは、列車の長さ分の300mだということがわかります。これがわかってしまえば、あとは「みはじ」の計算をするだけです。
道のり÷速さ=時間
300m÷秒速20m=15秒
よって答えは
15秒
絵を描いてもわからない場合は、おそらく速さの計算問題ができていないのだと思います。しっかり速さを定着させてから、もう一度トライしてみましょう。(速さの計算のやり方はこちら)
速さの問題なので、とりあえず「みはじ」の図をどこかに書いておきましょう。
まずは状況を整理します。
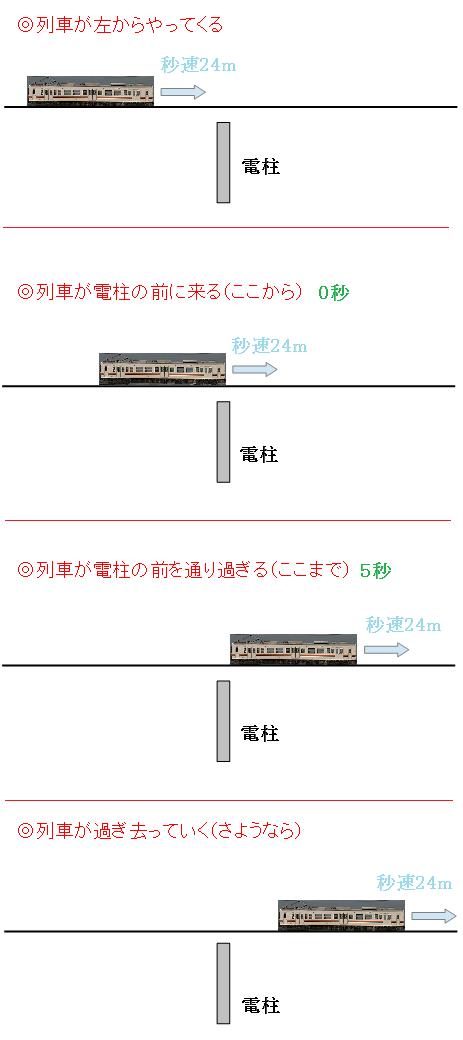
列車が左からやってきて、右に通り過ぎて行くまでの順を追うと図のようになります。続いて列車の先頭が電柱の前に来た瞬間と、列車の最後尾が電柱の前を通り過ぎて行く瞬間を並べてみましょう。
「みはじ」を使って、5秒間に進んだ道のりを出すと、
速さ×時間=道のり
秒速24m×5秒=120m
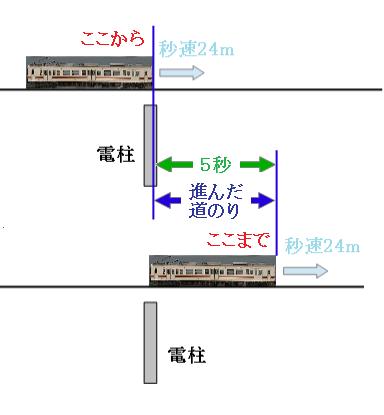
図を見ると、5秒間に列車が走った道のりと列車の長さは同じなので、答えは
120m
なお、列車の絵を描かずに写真にしたのは、決して上手に絵が描けなかったからではありません!!それでは、自分の前またはある地点を通過する通過算をまとめます。
続けて、鉄橋またはトンネルを通過する通過算を考えます。次もお絵かきお絵かき!
通過算② 鉄橋またはトンネルを通過する通過算の解き方
コツはただひとつ!絵を描くことです!(さっきも言った。)レッツお絵かきタイム!!
速さの問題なので、とりあえず「みはじ」の図をどこかに書いておきましょう。
まずは状況を整理します。
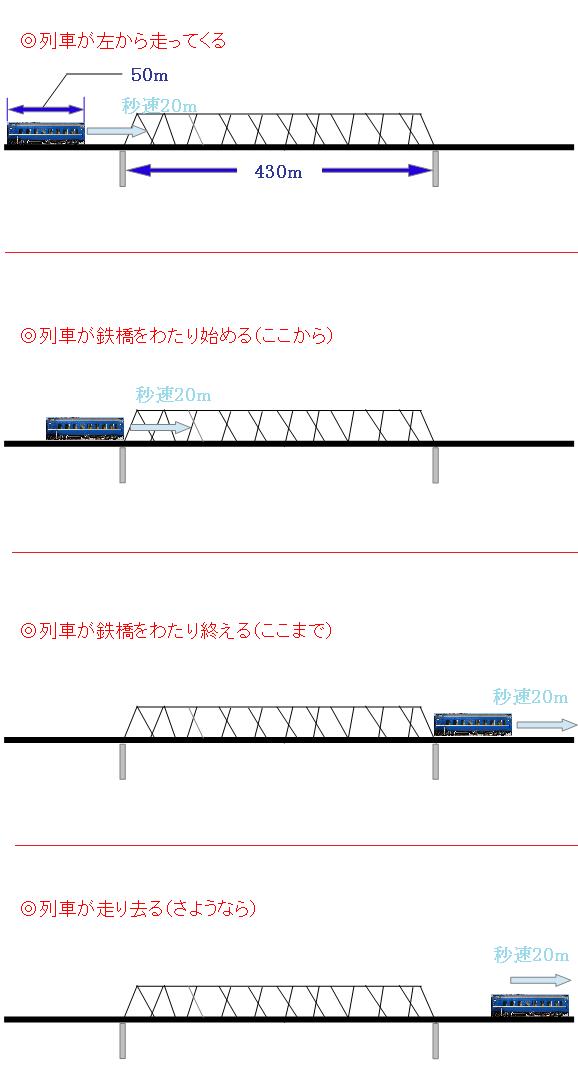
列車が左から走ってきて、鉄橋をわたり始めて、わたり終えて、走り去って行くまでを順に並べるとこんな感じです。 続けて、鉄橋をわたり始めた瞬間とわたり終えた瞬間を並べて、列車が走った道のりを考えてみましょう。
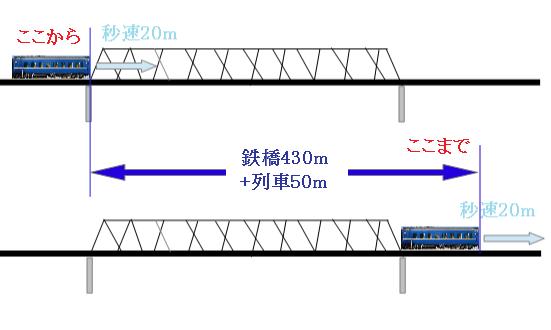
図のように、列車が走った道のりは鉄橋の長さ+列車の長さなので
430m+50m=480m
あとは、「みはじ」の公式を使って時間を出しましょう。
道のり÷速さ=時間
480m÷秒速20m=24秒
よって答えは
24秒
鉄橋が上手に描けました!ですが、問題を解くときは上手に描く必要はありません。あまり時間をかけていられないので、パパっと簡単に描けるように練習しましょう。
速さの問題なので、とりあえず「みはじ」の図をどこかに書いておきましょう。
まずは状況を整理します。
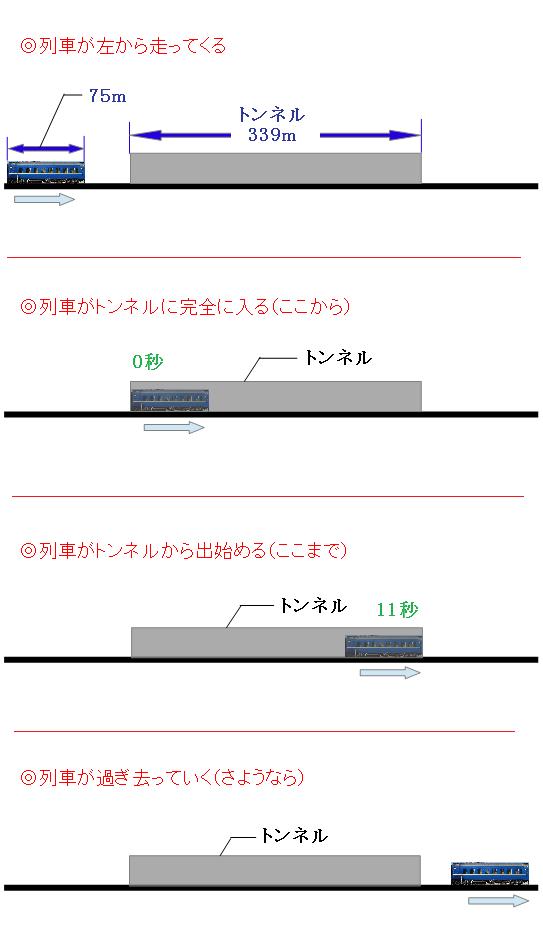
列車が左からやってきて、トンネルに完全に入り、トンネルから出始め、過ぎ去っていくまでを並べるとこんな感じです。 続いて、列車がトンネルに完全に入った瞬間と、トンネルから出始めた瞬間を並べて、列車が走った道のりを考えます。
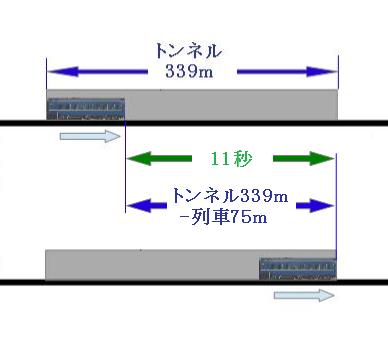
図のように、列車が実際に走った道のりはトンネルの長さよりも列車の長さ分短いので、
339m-75m=264m
あとは、「みはじ」の公式を使って速さを出しましょう。
道のり÷時間=速さ
264m÷11秒=秒速24m
秒速24mを、時速kmに直します。(速さの単位のかえ方はこちら)
秒速24m×3600秒
=時速86400m
=時速86.4km
よって答えは
時速86.4km
トンネルも上手に描けました!ということで、今回もお絵描きでした。それでは、鉄橋またはトンネルを通過する通過算をまとめましょう。
「自分の前またはある地点を通過する通過算」のまとめとまったく同じになってしまいました(´・ω・`)
続けて、列車がすれ違ったり、列車を追い越したりする通過算考えます。次もお絵かきお絵かき!
通過算③ 追いこしたりすれ違ったりする通過算の解き方
今回も基本的にお絵かきですが、動くものがふたつあるので少し工夫しなくてはなりません。さらに旅人算のような考え方も出てくるので、しっかりと旅人算をマスターしておきましょう!(旅人算の解き方はこちら)
速さの問題なので、とりあえず「みはじ」の図をどこかに書いておきましょう。
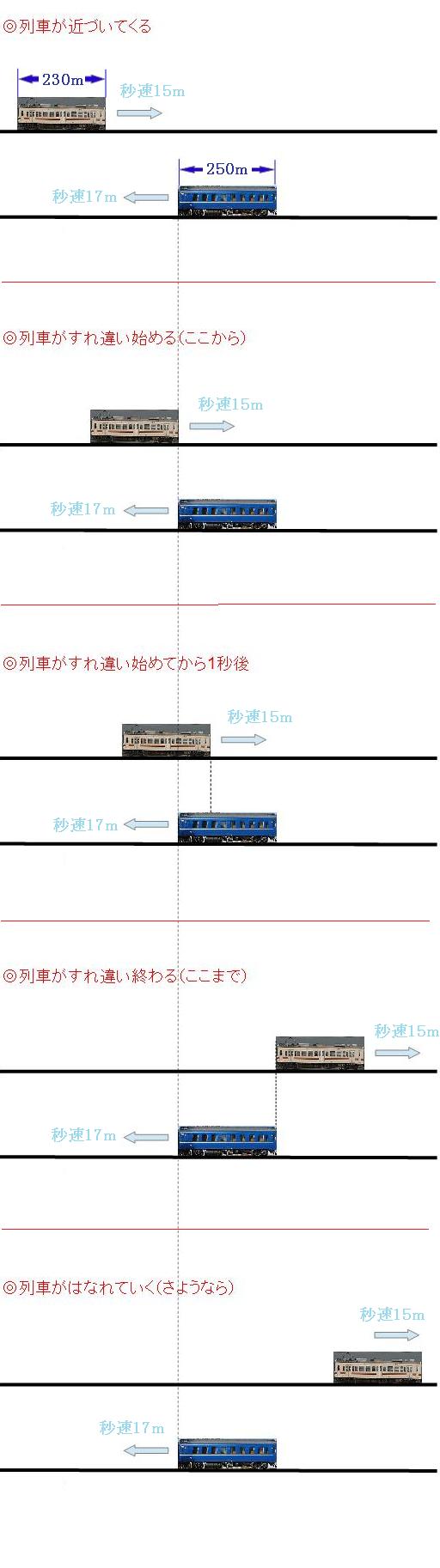
まずは状況を整理します。列車はどちらも動いているのですが、下りの列車(左に進む列車)を同じ場所に描いていきます。下り列車に合わせて、カメラも動いているイメージです。
列車が近づいてきて、すれ違い始め、すれ違ってから1秒経ち、すれ違い終わって、はなれて行くまでを並べるとこんな感じです。まずは、すれ違い始めとすれ違い終わりを並べて、2つの列車が走った道のりを考えてみましょう。
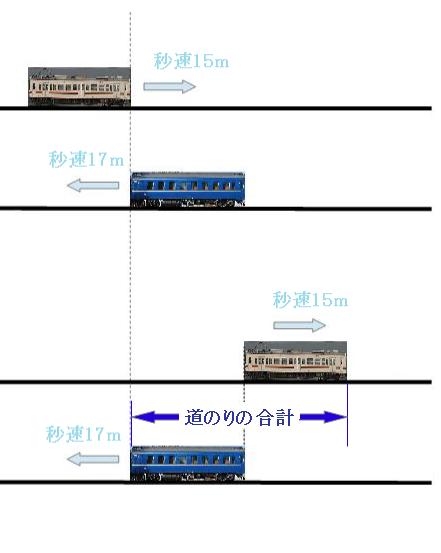
すれ違うのにかかった時間がわからないので、それぞれの列車が何m進んだのかはわからないのですが、旅人算と同じように、図を見ればふたつの列車が進んだ道のりの合計はわかります。ふたつの列車が進んだ道のりの合計は、ふたつの列車の長さの合計と同じなので
230m+250m=480m
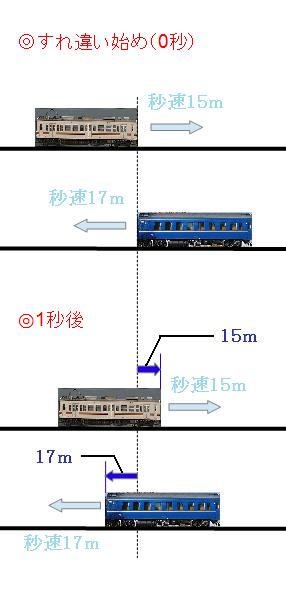
続いて、旅人算と同じように、すれ違い始めてから1秒後の状況を見てみましょう。ここの図だけ、カメラを固定して書いてみます。
上り電車は秒速15mなのでこの1秒間で15m進み、下り電車は秒速17mなのでこの1秒間で17m進みます。 したがって、図のようにこの1秒間で「15m+17m=32m」すれ違ったことになります。 ふたつの列車は、合わせて480mすれ違わなければならなかったので、すれ違いにかかる時間は、
480÷32=15
よって答えは
15秒
通過算なのでしっかりと絵を描いて道のりを考えることと、旅人算なので1秒後の状況を確認すること。このふたつのことに注意しながら解く必要があります。なお、旅人算と同じように、
すれ違いにかかる時間=長さの合計÷速さの合計
速さの合計=長さの合計÷すれ違いにかかる時間
長さの合計=すれ違いにかかる時間×速さの合計
と、考えてしまう人も多いです。ただし、こちらもただ暗記してしまうことはおすすめしません。練習問題をたくさん解いていれば、自然と頭がそういうふうに考えられるようになります。
速さの問題なので、とりあえず「みはじ」の図をどこかに書いておきましょう。
まずは状況を整理します。列車はどちらも動いているのですが、列車Bを同じ場所に描いていきます。列車Bに合わせて、カメラも動いているイメージです。
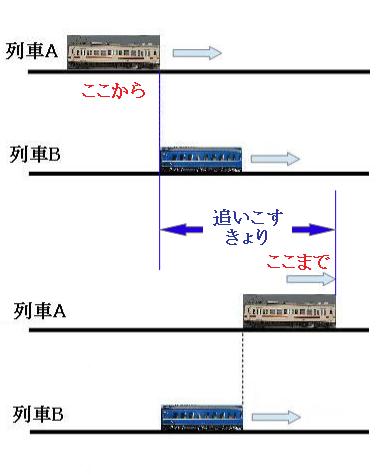
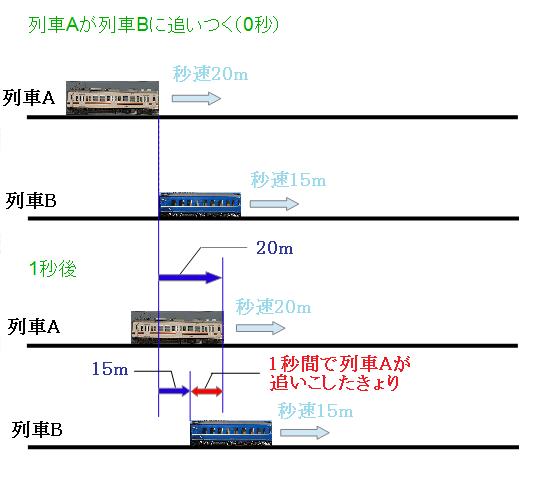
列車Aが列車Bに近づいていき、追いつき、追いついてから1秒経って、追いこし、はなれて行くまでを並べるとこんな感じです。 まずは、追いついたときと追いこした時を並べて、2つの列車が走った道のりを考えてみましょう。
追いこすまでにかかる時間がわからないので、2つの列車が進んだ道のりはわからないのですが、図を見れば列車Aが列車Bをどれだけ追いこしたかはわかります。列車Aが追いこしたきょりは、ふたつの列車の長さの合計と同じなので、
200m+150m=350m
それでは、列車Aが列車Bに追いついてから1秒後の状況を見てみましょう。ここの図だけ、カメラを固定して書いてみます。
この1秒間で列車Aは20m、列車Bは15m進みます。よって図のように、1秒間で列車Aは列車Bを「20m-15m=5m」追いこしたことになります。 全部で350m追いこさなければならないのでかかる時間は、
350÷5=70
よって答えは
70秒
最後の図がちょっとゴチャッとしてしまいました。もう少しスマートな図を書きたいところです。
追いこす問題でも、すれ違う問題と同じようにして、
追いこしにかかる時間=長さの合計÷速さの差
速さの差=長さの合計÷追いこしにかかる時間
長さの合計=追いこしにかかる時間×速さの差
と、覚えてしまう人もいます。それでは、追いこしたりすれ違ったりする通過算をまとめます。
ということで、お絵かきタイムでした。次は列車ではなくて、船です。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!