和差算
和差算とは
和差算とは、和や差がわかっている状態で、それぞれの個数を求める問題のことです。普通に考えると連立方程式を使う問題です。 算数では、これを線分図を使って考えます。個数や人数を求めることが多いので、線分図を書きやすい問題が多いです。 ここで線分図の書き方を練習しておくと良いと思います。
線分図については「線分図の書き方使い方。線分図が書けなきゃ算数は始まらない!」というページで解説しています。

線分図の書き方使い方。線分図が書けなきゃ算数は始まらない!
中学入試の算数で出題される「線分図」の書き方を解説しています。
和差算の解き方
和差算は、なにはともあれ線分図です。線分図が書けたら、出っ張っている部分を除いて考えるのがコツです。
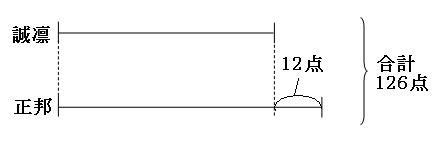
合計点がわかっていて、それぞれのチームの得点を求めるので、和差算の問題であることがわかります。和差算はなにはともあれ線分図なので、線分図を書いてみます。
線分図に書くと、状況が目で見えて安心します。続いて、出っ張っている部分を除いて考えてみます。
図のように、出っ張っている12点の部分を除くと、赤い点線四角の中は、
126点-12点=114点
と、なります。赤い点線四角の中には同じ長さの線が2本あるので、1本あたり、
114点÷2=57点
この57点の線の長さは、誠凛高校の得点の線の長さと同じなので、誠凛高校の得点は57点です。正邦高校は12点リードしているので、
57点+12点=69点
よって答えは
誠凛高校…57点、正邦高校…69点
まだまだ追いつける点差ですね!
線が2本ならば、線分図を書かなくても解けるかもしれません。3本以上になると、そもそも問題を読んだだけでは何を言っているのかよくわからなくなってしまうので、線分図を書いて状況を整理すると良いです。
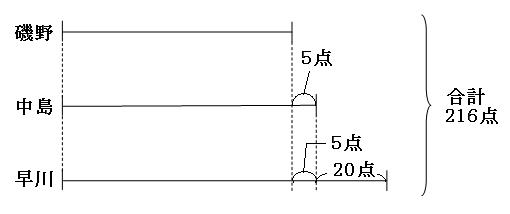
合計点がわかっていて、それぞれの点数を求めるので、和差算の問題であることがわかります。 3人登場すると問題を読んでもよくわかりませんが、ここで「わからない(´・ω・`)」と言わずに、線分図を書いてみましょう。書いてみると意外とわかるものです。
線分図に書くと、状況が目で見えて安心します。続いて、出っ張っている部分を除いて考えてみます。
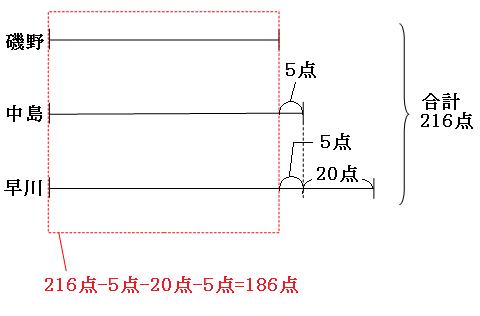
赤い点線四角からはみ出してしまっているのは、中島君が5点、早川さんが20点+5点=25点です。よって赤い点線四角の中は、
216点-5点-25点=186点
赤い点線の四角の中には同じ長さの線が3本あるので、1本あたり、
186点÷3=62点
この62点の線の長さは、磯野くんの点数の長さと同じなので、磯野くんは62点だったことがわかりました。
早川さんの線は、磯野君の線よりも25点ぶん長いので、
62点+25点=87点
よって答えは
87点
人数が4人や5人になることもありますが、しっかりと問題を読んで線分図を書けば、解き方は基本的にはすべて同じです。 それでは和差算をまとめます。
次も似たような線分図のお話です。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!