分配算
分配算とは
分配算は、前のページで解説した和差算によく似て、和や差がわかっている状態で、それぞれの数量を求めます。 ただ、分配算が「○個多い」などの数量の関係だったものが、「○倍あります」や、「○:△になります」のような、比の関係が混ざってきます。 和差算よりも、少しだけ線分図の書き方が難しいかもしれません。線分図がちょっと不安だという人は、もう少し和差算で線分図を練習してからトライしましょう。
分配算の解き方
分配算も、なにはともあれ線分図です。あれこれ考える前に、まず線分図を書いてみましょう。 コツは、和差算と似ていて、出っ張っている部分を除いたり、へこんでいる部分を足したりすることと、比の①にあたる数量を求めることです。
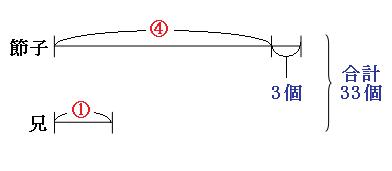
まずは線分図を書いてみます。「4倍」と書いてある部分は「1:4」と考えて線分図を書きます。
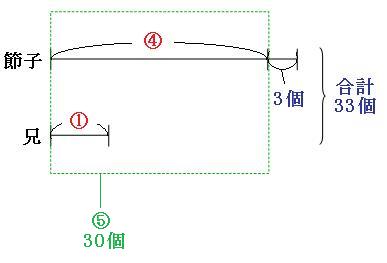
続いて、出っ張っている「3個」の部分を除いて考えてみます。
図のように、出っ張っている3個の部分を除くと、緑の点線四角の中は、
ドロップの個数
33個-3個=30個
比
①+④=⑤
と、なります。緑の点線四角の中には、比に関しては⑤、個数に関しては30個なので、①あたりのドロップの個数を求めると、
30個÷⑤=6個
で、①が6個にあたることがわかりました。節子の線分図を見てみると、④よりも3個ぶん長いので、
6個×④+3個=27個
よって答えは
27個
ホタル、なんですぐ(略)。
線分図のどこの部分を考えれば①を求められるのかが見えれば簡単です。このあとも、①がいくつにあたるのかを求める問題がたくさん出てきます。
中には線分図が複雑で、注目すべき場所をなかなか見つけられない問題も出てきます。分配算のところで、しっかりと練習しておきましょう。
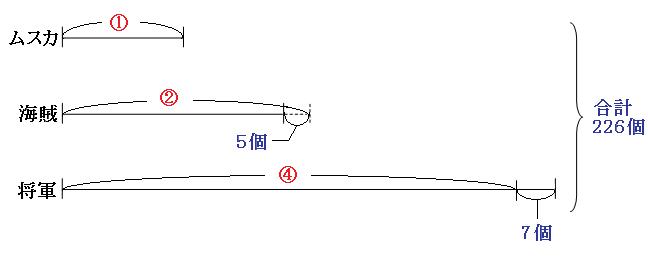
まずは線分図を書いてみます。
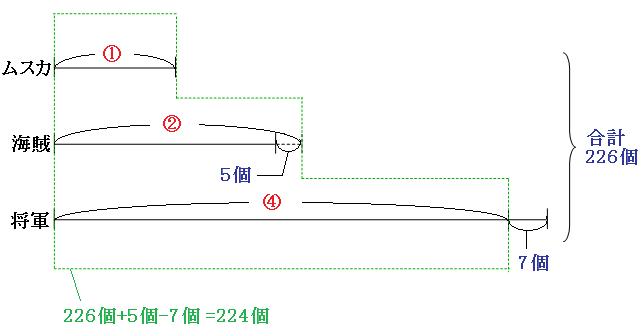
続いて、海賊のへこんでいるところを足し、将軍の出っ張っているところを除いて考えてみます。
図のように、海賊のへこんでいる5個を足し、将軍の出っ張っている7個を引くと、緑の点線四角の中は、
宝物の数
226個+5個-7個=224個
比
①+②+④=⑦
と、なります。緑の点線四角の中には、比に関しては⑦、個数に関しては224個なので、①あたりの宝物の個数を求めると、
224個÷⑦=32個
で、①が32個にあたることがわかりました。将軍の線分図を見てみると、④よりも7個ぶん長いので、
32個×④+7個=135個
よって答えは
135個
手にした宝を、無事に持って帰れるといいですね。
こちらの問題も、「どこに注目すれば①を求められるか」に注意して解くと簡単です。
あまりに①を求めるので、「マルイチ算」と呼ばれることもあるそうです。
それでは分配算をまとめます。
次も似たような線分図の問題です。年齢のお話です。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!