通過算の練習問題③ 応用編
通過算の応用問題
こちらは、通過算の応用問題を載せているページです。
通過算の詳しい解説はこちら、基本問題はこちら、標準問題はこちらへどうぞ。
通過算のポイントは、絵を描いて、実際に走った道のりを求めることです。
とりあえず、速さの単位を変換しておきます。時速kmを秒速mに直します。
時速68.4km=秒速19m
時速43.2km=秒速12m
(速さの単位変換の方法はこちら)
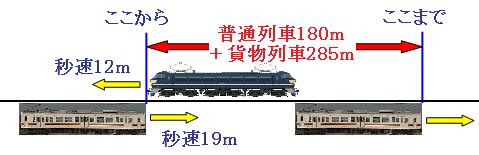
普通列車と貨物列車がすれ違い始めた時と、すれ違い終わった時の絵を描いて、2つの列車の進んだ道のりの合計を考えます。 本当はどちらの列車も動いているのですが、どちらも動かしてしまうと絵がゴチャゴチャになってしまうので、今回は貨物列車を同じ場所に描きます。
図のように、出会ってからすれ違うまでに進んだ2つの列車の道のりの合計は、
180m+285m=465m
ここからは旅人算の考え方です。(旅人算の解説はこちら)
普通列車は1秒間に19m、貨物列車は1秒間に12m進むので、1秒間にすれ違う道のりは、
19m+12m=31m
全部で465mすれ違うので、かかる時間は、
465m÷31m=15
よって答えは
15秒
とりあえず、速さの単位を変換しておきます。時速kmを秒速mに直します。
時速90km=秒速25m
時速72km=秒速20m
(速さの単位変換の方法はこちら)
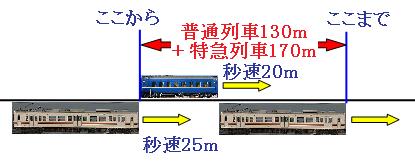
特急列車が普通列車に追いついた時と、普通列車を完全に追いこした時の絵を描いて、2つの列車の進んだ道のりの差を考えます。 本当はどちらの列車も動いているのですが、どちらも動かしてしまうと絵がゴチャゴチャになってしまうので、今回は普通列車を同じ場所に描きます。
図のように、追いついてから追いこすまでに進んだ2つの列車の道のりの差は、
170m+130m=300m
つまり、特急列車の方が、普通列車よりも300m多く走ったということになります。ここからは旅人算の考え方です。(旅人算の解説はこちら)
特急列車は1秒間に25m、普通列車は1秒間に20m進むので、1秒間に追いこす道のりは、
25m-20m=5m
全部で300m追いこすので、かかる時間は、
300m÷5m=60
よって答えは
60秒
とりあえず、速さの単位を変換しておきます。時速kmを秒速mに直します。
時速79.2km=秒速22m
時速64.8km=秒速18m
(速さの単位変換の方法はこちら)
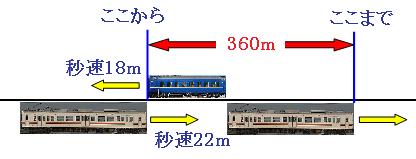
特急列車は1秒間に22m、普通列車は1秒間に18m進むので、1秒間にすれ違う道のりは、
22m+18m=40m
9秒かかってすれ違うので、2つの列車が進んだ道のりの合計は、
40m×9秒=360m
普通列車と貨物列車がすれ違い始めた時と、すれ違い終わった時の絵を描いてみます。 本当はどちらの列車も動いているのですが、どちらも動かしてしまうと絵がゴチャゴチャになってしまうので、今回は普通列車を同じ場所に描きます。
図のように、出会ってからすれ違うまでに進んだ2つの列車の道のりの合計は、列車の長さの和になっています。特急列車の長さは190mなので、普通列車の長さは、
360m-190m=170m
よって答えは
170m
とりあえず、速さの単位を変換しておきます。時速kmを秒速mに直します。
時速72km=秒速20m
(速さの単位変換の方法はこちら)
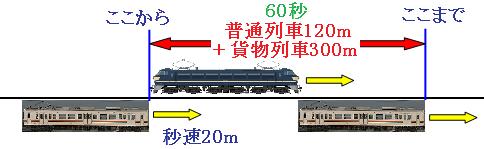
普通列車が貨物列車に追いついた時と、貨物列車を完全に追いこした時の絵を描いて、2つの列車の進んだ道のりの差を考えます。 本当はどちらの列車も動いているのですが、どちらも動かしてしまうと絵がゴチャゴチャになってしまうので、今回は貨物列車を同じ場所に描きます。
図のように、追いついてから追いこすまでに進んだ2つの列車の道のりの差は、
300m+120m=420m
つまり、普通列車の方が、貨物列車よりも420m多く走ったということになります。
追いこすのにかかった時間は1分(60秒)なので、1秒間で追いこす道のりは、
420m÷60秒=7m
普通列車は1秒間で20m進みますので、貨物列車が1秒間で進む道のりは、
20m-7m=13m
よって、貨物列車の速さは秒速13mです。答えは時速kmで答えるので、
秒速13m=時速46.8km
よって答えは
時速46.8km
①すれ違う時
出会ってからすれ違うまで、2つの列車が進んだ道のりの合計は、
208m+160m=368m
すれ違うのにかっかた時間は8秒なので、1秒間ですれ違った道のりは、
368m÷8秒=46m
つまり、特急列車と普通列車が1秒間に進む道のりの和は46mです。
②追いこす時
追いついてから追いこすまで、2つの列車が進んだ道のりの差は、
208m+160m=368m
追いこすのにかっかた時間は3分4秒(184秒)なので、1秒間で追いこした道のりは、
368m÷184秒=2m
つまり、特急列車と普通列車が1秒間に進む道のりの差は2mです。
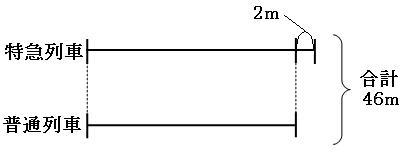
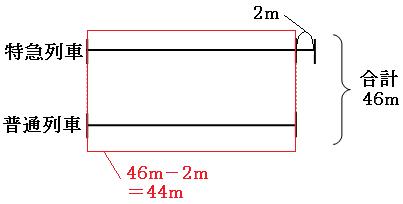
③1秒間に進む道のりの和と差が分かったので
和と差が分かっているので、和差算を使います。(和差算の解説はこちら)
さっそく線分図を書いてみましょう。
この線分図を使って、普通列車が1秒間に進む道のりを求めます。
線分図より普通列車が1秒間に進む道のりは、
(46m-2m)÷2=22m
よって、特急列車が1秒間に進む道のりは、
22m+2m=24mよって答えは
特急列車…秒速24m
普通列車…秒速22m
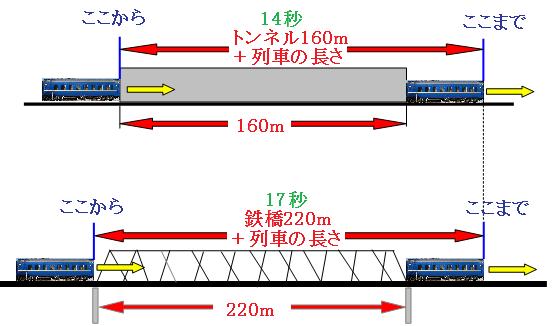
コツは、「ここまで」の地点をたてに合わせて描くことです。この2つの絵を見比べてみましょう。
この絵の、緑の矢印の部分に注目してみます。この部分は、
時間
17秒-14秒=3秒
道のり
220m-160m=60m
つまり、この列車は3秒間で60m進むので、速さは、
60m÷3秒=秒速20m
続いて、列車の長さを求めます。速さを求めたので、トンネルを使っても鉄橋を使っても、普通の通過算の考え方で求められます。今回はトンネルの方を使ってみます。
トンネルを通りすぎるのには14秒かかっていますので、その間に列車が進んだ道のりは、
秒速20m×14秒=280m
トンネルの長さは160mだったので、列車の長さは、
280m-160m=120m
よって答えは
速さ…秒速20m
長さ…120m
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!