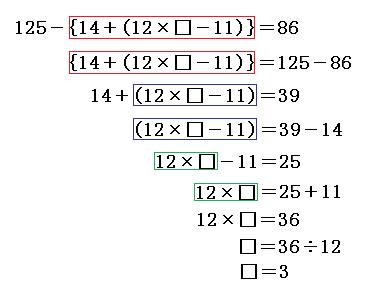基本 □を求める計算
□を求める計算の基本
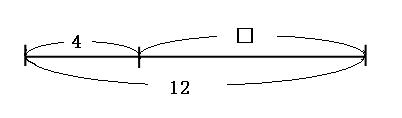
「4+□=12」のように、式のなかに□が入っていて、その□の中に入る数字を求める問題を還元算といいます。 この例の場合は、「4にいくつ足したら12になるだろう?」と考えます。
上の図を見ると、□は「12-4」で求められることがわかります。このように、たし算に□が入っていた場合は、ひき算をすると□の中の数字を求めることができます。 ひき算、かけ算、わり算の時も、同じように考えることができます。
- たし算のとき
引き算をする。 - かけ算のとき
わり算をする。 - 引き算のとき
□が左にあればたし算を、□が右にあればひき算をする。 - わり算のとき
□が左にあればかけ算を、□が右にあればわり算をする。
なぜ上に書いたような方法で□を求めることができるかは、例題を使ってイメージしてみましょう。
① □÷12=8
わり算で、左に□があるので、かけ算をします。
□=8×12
□=96
□=96
なぜこのような計算で□が求められるのか考えてみましょう。
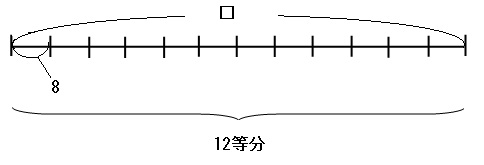
元の式「□÷12=8」のイメージは、「□個のものを12人に分けたら、1人8個ずつ配れた」という感じです。これを線分図に表すと下のようになります。
上の線分図を見ると、8に12をかければ□を求められることがわかりやすいですね。
② 144÷□=12
わり算で、右に□があるので、わり算をします。
□=144÷12
□=12
□=12
なぜこのような計算で□が求められるのか考えてみましょう。
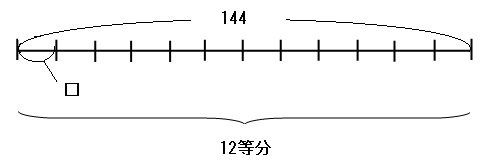
元の式「144÷□=12」のイメージは、「144個のものを□個ずつに分けたら、12等分に分けられた」という感じです。これを線分図に表すと下のようになります。
上の線分図を見ると、144を12で割れば□を求められることがわかりやすいですね。
③ 23-□=5
ひき算で、右に□があるので、ひき算をします。
□=23-5
□=18
□=18
なぜこのような計算で□が求められるのか考えてみましょう。
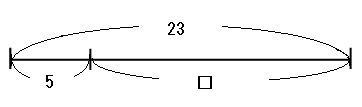
元の式「23-□=5」を線分図に表すと下のようになります。
上の線分図を見ると、23から5を引けば□を求められることがわかりやすいですね。
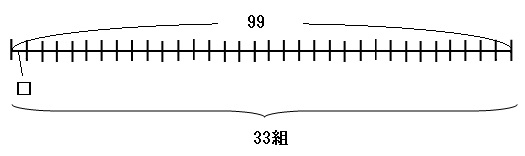
④ □×33=99
かけ算なので、わり算をします。
□=99÷33
□=3
□=3
なぜこのような計算で□が求められるのか考えてみましょう。
元の式「□×33=99」のイメージは、「□個のものを33組用意すると、全部で99個になった」という感じです。これを線分図に表すと下のようになります。
上の線分図を見ると、99を33で割れば□を求められることがわかりやすいですね。
□を求める計算の順序
式が長くなると、計算する順番を考えなくてはいけなくなります。が、計算練習をしっかりとやっていれば難しいことはありません。
□を求めるときは、普段の計算の逆の順番で考えていきます。
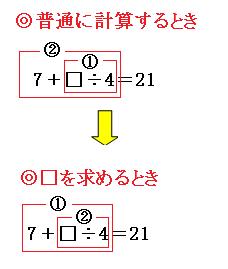
7+□÷4=21
たし算とわり算が混ざっているので、普段は「①わり算、②たし算」の順番で計算をしていきます。
□を求めるときはその逆で「①たし算、②わり算」の順番で考えていきます。
「□÷4」の部分を大きな□と見て、「7+□」になっていると考えます。たし算なので、□を求めるときはひき算をすればいいわけです。
よっと答えは
□=56
「計算の順番が普段と逆になる」ことと、「大きな□と見る」ことができれば、どんなに複雑な式が出てきても求められますよ!
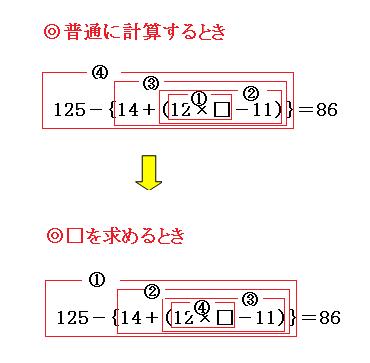
5×25-{14+(12×□-11)}=86
とりあえず、「5×25」の部分は計算できるので、計算しておきます。
5×25-{14+(12×□-11)}=86
125-{14+(12×□-11)}=86
それでは計算の順序を考えましょう。
それでは、この順番で求めていきましょう。
よっと答えは
□=3
□の代わりに、「a、b、x、y」などのアルファベットが使われることもあります。求め方は全く変わらないので安心してください。
しかも、アルファベットで書くとかっこよく見えます。
それでは、□を求める計算をまとめます。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!