分数の基本をわかりやすく解説。「分数とは何か」を意識できれば超便利!
分数とは
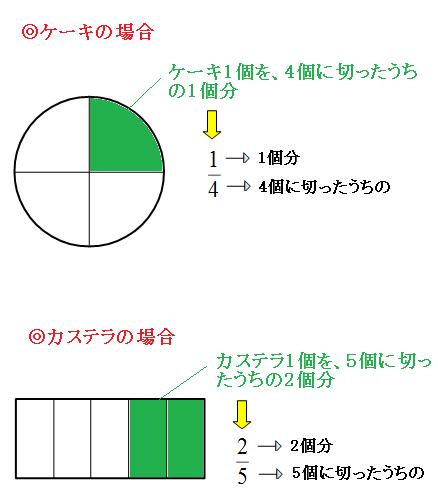
分数とは、「1つの物を、何個に切ったうちの何個分」と表すことができる数字です。はじめのうちは、分数が出てくるたびに「何個に切ったうちの何個分」と頭の中で考えて、だいたいどれくらいの大きさの数なのか想像するようにしましょう。 実際に絵を書いて考えてもよいと思います。想像するものは、ケーキでもカステラでもうまい棒でも大丈夫です。
あまり注目されないのですが、分数を見た時に上のような絵を想像できるようになれば、分数はマスターしたも同然です。
「分数が苦手」と感じるのは、数字を見てもどれくらいの大きさなのかが分かっていないからです。まずは、このイメージを作る練習しましょう。
話は飛びますが、分数の上と下には名前がついていて、下の数字を分母、上の数字を分子といいます。

分数の種類
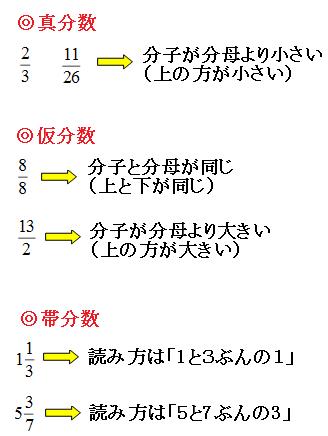
分数には、3種類の分数があります。
- 分子の数が分母の数よりも小さい真分数。
- 分子の数が分母の数と同じか、または大きい仮分数。
- 整数と分数がくっついた帯分数。
帯分数を仮分数に直す方法
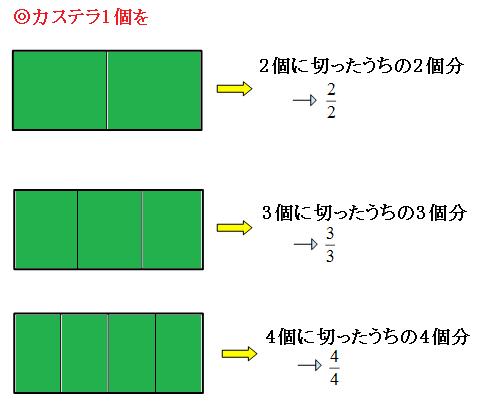
まずは、1を分数で表すとどうなるのか考えてみましょう。
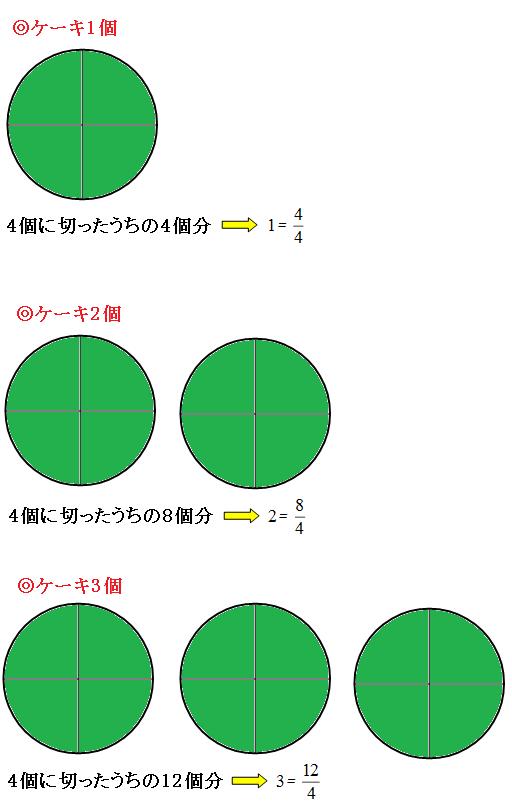
つまり、分母の数と分子の数が同じならば「1」になります。では、他の整数はどうなるでしょうか。
つまり、整数を分数に直すときは、「分子の数=分母の数×整数」になります。
| (1)1 | = | □ | |
| 3 |
| (2)3 | = | □ | |
| 6 |
| (3)15 | = | □ | |
| 9 |
| (1)1 | = | □ | |
| 3 |
分母と分子が同じ数字だと、その分数は「1」になるので、
| 1 | = | 3 | |
| 3 |
よって答えは
□=3
| (2)3 | = | □ | |
| 6 |
分子がいくつになるかを考えましょう。整数を分数に直すときは、「分子の数=分母の数×整数」なので、
分子の数=分母の数×整数
=6×3
=18
なので、
| 3 | = | 18 | |
| 6 |
よって答えは
□=18
| (3)15 | = | □ | |
| 9 |
分子を求めましょう。
分子の数=分母の数×整数
=9×15
=135
なので、
| 15 | = | 135 | |
| 9 |
よって答えは
□=135
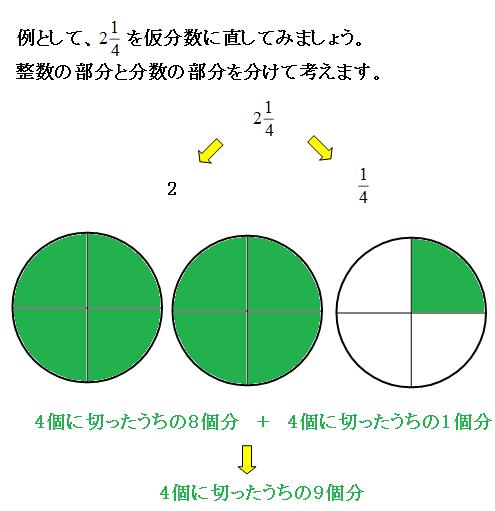
それではいよいよ帯分数を仮分数に直してみます。ここまでが理解できていれば、あとはチョチョイのチョイのチョイです!
帯分数は、整数と分数がくっついていますが、整数の部分と分数の部分を分けて考えることができます。
| なので、2 | 1 | = | 9 | となります。 | ||
| 4 | 4 |
まとめると、帯分数を仮分数に直すときは、「仮分数の分子の数=分母の数×整数の部分+帯分数のときの分子の数」になります。
| (1)1 | 1 | |
| 5 |
| (2)3 | 2 | |
| 3 |
| (3)12 | 13 | |
| 15 |
| (1)1 | 1 | |
| 5 |
分子がいくつになるのかを考えましょう。帯分数を仮分数に直すときは、「仮分数の分子の数=分母の数×整数の部分+帯分数のときの分子の数」なので、
仮分数の分子の数=分母の数×整数の部分+帯分数のときの分子の数
=5×1+1
=6
なので、
| 1 | 1 | = | 6 | |
| 5 | 5 |
よって答えは
6 5
| (2)3 | 2 | |
| 3 |
分子を求めましょう。
仮分数の分子の数=分母の数×整数の部分+帯分数のときの分子の数
=3×3+2
=11
なので、
| 3 | 2 | = | 11 | |
| 3 | 3 |
よって答えは
11 3
| (3)12 | 13 | |
| 15 |
分子を求めましょう。
仮分数の分子の数=分母の数×整数の部分+帯分数のときの分子の数
=15×12+13
=193
なので、
| 12 | 13 | = | 193 | |
| 15 | 15 |
よって答えは
193 15
仮分数を帯分数に直す方法
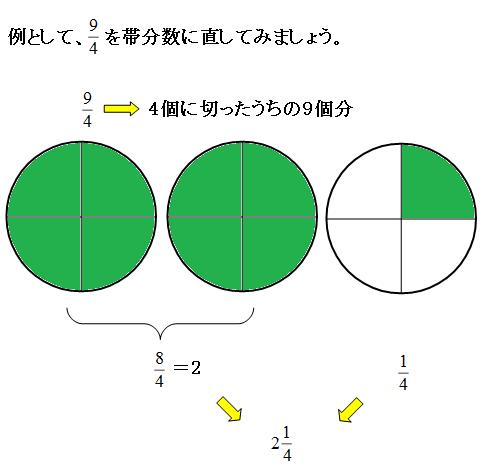
帯分数を仮分数に直すことができるのなら、逆は簡単です。同じように考えれば大丈夫です。
| よって、 | 9 | = | 2 | 1 | |
| 4 | 4 |
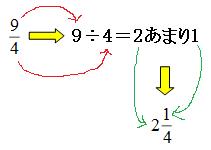
はじめはちゃんとイメージをしながら考えてほしいのですが、実際に計算をするときには、「分子÷分母をして、答えが整数の部分、あまりが分子」と考えてしまいます。
| (1) | 9 | |
| 7 |
| (2) | 46 | |
| 3 |
| (3) | 6347 | |
| 29 |
| (1) | 9 | |
| 7 |
分子÷分母をします。
9÷7=1あまり2
なので、
| 9 | = | 1 | 2 | |
| 7 | 7 |
よって答えは
1 2 7
| (2) | 46 | |
| 3 |
分子÷分母をします。
46÷3=15あまり1
なので、
| 46 | = | 15 | 1 | |
| 3 | 3 |
よって答えは
15 1 3
| (3) | 6347 | |
| 29 |
分子÷分母をします。
6347÷29=218あまり25
なので、
| 6347 | = | 218 | 25 | |
| 29 | 29 |
よって答えは
218 25 29
約分
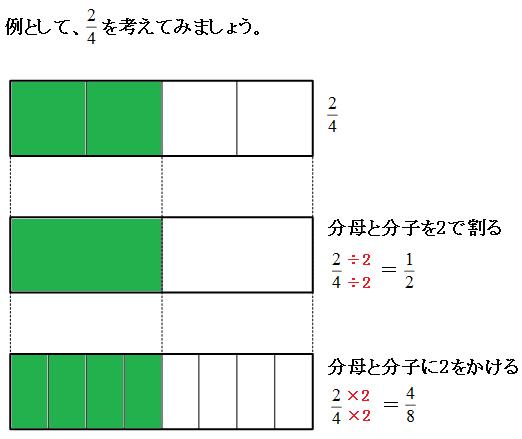
分数には、「分母と分子に同じ数をかけ算しても、同じ数でわり算しても、大きさは変わらない」という性質があります。
特に、分母と分子を同じ数でわり算して、なるべく小さな数にすることを約分といいます。分数はできるだけ約分をするのがマナーです。 分数が出てきたら、いつでも「約分できるかな?」って考えるようにしましょう。
| (1) | 3 | |
| 6 |
| (2) | 18 | |
| 24 |
| (3) | 63 | |
| 108 |
| (1) | 3 | |
| 6 |
分母と分子を3で割ります。
| 3 | = | 1 | |
| 6 | 2 |
よって答えは
1 2
| (2) | 18 | |
| 24 |
分母と分子を6で割ります。
| 18 | = | 3 | |
| 24 | 4 |
今回ははじめから6でわり算をしましたが、2で割ってから、そのあとで3で割ってもかまいません。一度にやらずに、何回かに分けてわり算をしても大丈夫です。

よって答えは
3 4
| (3) | 63 | |
| 108 |
分母と分子を9で割ります。
| 63 | = | 7 | |
| 108 | 12 |
よって答えは
7 12
通分
「分母と分子に同じ数をかけ算しても、大きさは変わらない」性質を使って、2つ以上の分数の分母を同じ数にそろえることを通分といいます。 分母は、最小公倍数でそろえるようにします。
| (1) | 1 | , | 1 | |
| 2 | 3 |
| (2) | 3 | , | 2 | |
| 10 | 15 |
| (3) | 2 | , | 1 | , | 7 | |
| 5 | 6 | 12 |
| (1) | 1 | , | 1 | |
| 2 | 3 |
分母は「2」と「3」なので、最小公倍数の「6」でそろえます。

よって答えは
3 , 2 6 6
| (2) | 3 | , | 2 | |
| 10 | 15 |
分母は「10」と「15」なので、最小公倍数の「30」でそろえます。

よって答えは
9 , 4 30 30
| (3) | 2 | , | 1 | , | 7 | |
| 5 | 6 | 12 |
分母は「5」と「6」と「12」なので、最小公倍数の「60」でそろえます。

よって答えは
24 , 10 , 35 60 60 60
わり算と分数
分数は「分子÷分母」のわり算にすることができます。例えば、
| 8 | = | 8÷2 | = | 4 | |
| 2 |
この法則を使えば、分数を小数に直すことが出来ます。
| (1) | 3 | |
| 8 |
| (2) | 12 | |
| 5 |
| (3)2 | 1 | |
| 4 |
| (1) | 3 | |
| 8 |
分子÷分母を計算します。
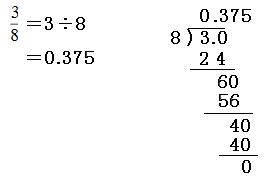
よって答えは
0.375
| (2) | 12 | |
| 5 |
分子÷分母を計算します。
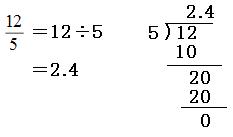
よって答えは
2.4
| (3)2 | 1 | |
| 4 |
整数の部分と分数の部分を分けて、分数の部分は分子÷分母を計算します。
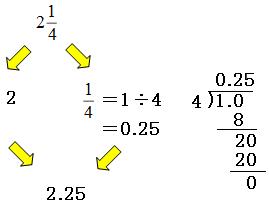
よって答えは
2.25
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!