割合の基本を解説。割合の計算問題は算数というより国語の問題!
割合とは
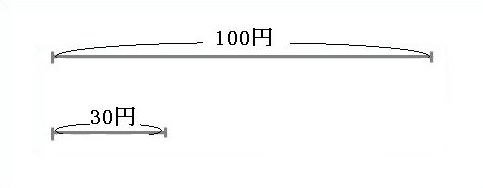
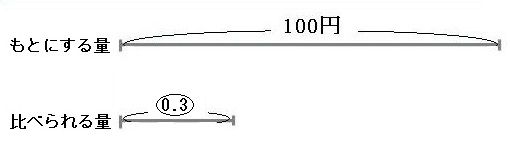
大きさや量を比べる時、いろいろな方法がありますが、「何倍になるか」で比べる方法を割合といいます。 例えば、100円と30円を比べてみましょう。
となります。
これで、30円は100円の0.3倍であることがわかりました。
基準にした100円の方(①にした方)をもとにする量、比べた30円の方を比べられる量、求めた「0.3倍」の0.3を割合と言います。
割合の表し方
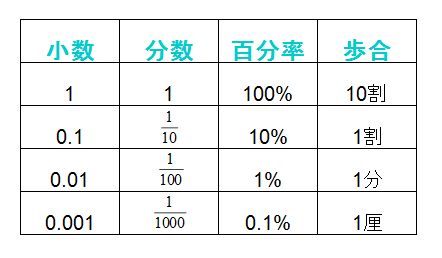
割合の表し方はいくつかあり、先ほど求めた小数の形もあれば、分数、百分率(%)、歩合(○割○分)でも表されます。 表し方を表にまとめてみます。
例えば
0.13=13%=1割3分
0.049=4.9%=4分9厘
0.703=70.3%=7割3厘
です。
特に歩合に関してはあまり慣れていないと思うので、練習して慣れておきましょう。
野球の打率やバーゲンセールの割引などでよく使われるものですので、日常生活でも目にする機会は多いと思います。
見かけた時は、「何%かな?」って考えてみましょう。
割合の計算
先程も書きましたが、割合の問題には3つの要素があります。「もとにする量」「比べられる量」「割合」です。 速さと同じく、この3つの内の2つがわかっていれば、もう1つは計算で求められます。
割合の求め方
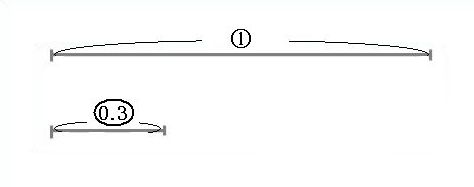
冒頭で簡単に割合を求めてしまいましたが、もう一度割合の求め方をしっかりと考えてみましょう。100円と30円を比べてみます。100円をもとにする量とし、30円の割合を求めてみましょう。
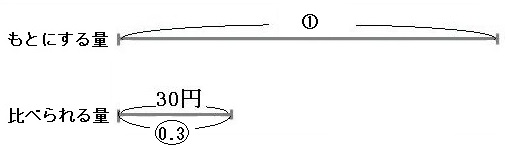
割合は、もとにする量を①として、比べられる量がいくつに当たるかを考えます。
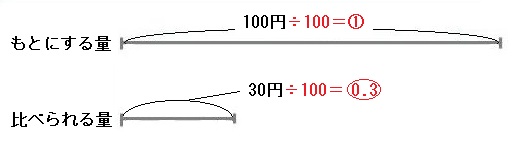
100円を①にするためには100で割らなくてはなりません。もとにする量を100で割ったので、比べられる量も同じように100で割ります。
30÷100=0.3
これで100円に対する30円の割合が0.3であることが求められました。
0.3は「30%」や「3割」と言い換えることもできます。
今回計算した「30÷100」は、「比べられる量」を「もとにする量」で割ったことになります。よって、割合の求め方を公式にすると、
割合=比べられる量÷もとにする量
比べられる量の求め方
「もとにする量」と「割合」がわかっていれば、「比べられる量」を求めることができます。
例えば、もとにする量を100円として、その30%がいくらに当たるか考えてみましょう。30%は、小数であらわすと0.3になります。
このページの一番最初で説明をしましたが、「何倍になるか」で比べる方法を割合といいます。
今回は「もとにする量」が100円で、「割合」が0.3ということなので、もとにする量「100円」の0.3倍が比べられる量になります。
つまり比べられる量は
100円×0.3=30円
で、30円になることが分かりました。
これは、「比べられる量」と「割合」のかけ算になります。よって、比べられる量の求め方を公式にすると、
比べられる量=もとにする量×割合
ここでひとつ注意が必要なのですが、割合は必ず小数か分数で計算してください。百分率や歩合のまま計算をしないでください。例えば今回の例題で、
100円×30%=3000円
と、すると間違いになります。初心者に多いミスなので、気をつけてください。
もとにする量の求め方
「比べられる量」と「割合」がわかっていれば、「もとにする量」を求めることができます。
「比べられる量」を30円、「割合」を30%として、「もとにする量」を求めてみましょう。30%は、小数で表すと0.3になります。
このページのはじめの方に書きましたが、もとにする量は①になります。つまり、上の線分図の①がいくらに当たるかを考えます。
そのために、0.3にどんな計算をすれば1になるかを考えます。
ここで、同じ数を割り算すると答えは1になるという性質を使います。
例えば、「15÷15=1」ですし、「12.5÷12.5=1」になります。同じようにして、「0.3÷0.3=1」となります。
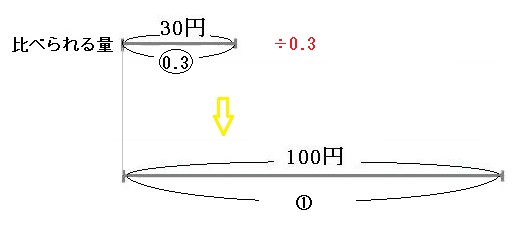
つまり、先ほどの線分図の比べられる量の線分図を0.3で割ると、①を求めることができます。
割合
0.3÷0.3=1
お金
30円÷0.3=100円
これで①が100円に当たることがわかりました。先ほど説明したとおり、もとにする量は①になります。つまり、これでもとにする量が100円であることが求められました。
今回計算した「30円÷0.3」は、「比べられる量」を「割合」で割ったことになります。よって、もとにする量の求め方を公式にすると、
もとにする量=比べられる量÷割合
もう一度書きますが、割合は必ず小数か分数で計算してください。百分率や歩合のまま計算をしないでください。例えば今回の例題で、
30円÷30%=1円
と、すると間違いになります。初心者はこのミスが本当に多いです。本当に本当に本当に気をつけてください。
割合の計算の魔法の図
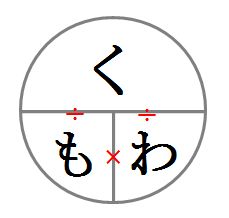
速さの「みはじ」と同じように使えます。「くもわ」と覚える人が多いと思います。「く」が「比べられる量」、「も」が「もとにする量」、「わ」が「割合」を示します。「みはじ」の時と同じように、求めたいものを隠して使います。
比べられる量=もとにする量×割合
もとにする量=比べられる量÷割合
割合=比べられる量÷もとにする量
と、なります。ただし注意してもらいたいのは、計算をする時は割合は必ず小数か分数を使います。百分率や歩合のままの数字で計算しないようにしましょう(耳にタコ)。
この「くもわ」も、「みはじ」の図と同じように時間の短縮のために使ってください。とても便利です。
ただし、最初は必ず「割合は何倍になるかで比べている」「もとにする量を①にする」ということをしっかり考えながら練習してください。くもわの図にたよりすぎると、応用問題に対応できなくなってしまいます。
どれがもとにする量?
速さの計算ができていれば、割合の計算は難しくありません。百分率のまま計算してしまって間違えるくらいです。
にも関わらず割合を苦手とする人が多いのは、割合の3つの要素のどれがどれなのか読み取れていない人が多いからです。
割合には「%」や「割」などがついていることが多いのですぐに見分けられるのですが、特に「もとにする量」と「比べられる量」がわからなくなってしまうことが多いようです。
一応、問題文の「の」の前が「もとにする量」であるという裏技があるのですが、出題者の方も手を変え品を変え文章を変えひっかけてきます。 ですので、ちゃんと文章を読んで判断できるように練習することをおすすめします。
算数を解いてる間は、頭が算数モードになっていて、文章の読みがおろそかになることがあります。
ですが、算数においても文章をしっかりと読み取ることは非常に重要です。しっかりと読み込みましょう。
問題文に(く)(も)(わ)を書き込めたら、割合の計算問題はマスターしたも同然です。
100円を基準にすると(①と置くと)、8円は0.08に当たるという意味なので
(も)100円の(わ)8%は(く)8円である。
となる。
90kgを基準にすると(①と置くと)、36kgは0.4に当たるという意味なので
(く)36kgは(も)90kgの(わ)40%である。
となる。
食塩水200gを基準にすると(①と置くと)、食塩10gは5%に当たるという意味なので
(わ)5%の食塩水(も)200gには、(く)10gの食塩が溶けている。
となる。
バファリン全体を基準にすると(①と置くと)、優しさは半分に当たるという意味なので
(も)バファリンの(わ)半分は(く)優しさでできている。
となる。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!