時計算の練習問題① 基礎編

時計算の基本問題
こちらは、時計算の基本問題を載せているページです。
時計算の詳しい解説はこちら、標準問題はこちら、応用問題はこちらへどうぞ。
時計算のポイントは、1分間で長針は短針に5.5°ずつ追いつく、またははなれていくことです。
(基本問題1)5時20分のとき、長針と短針がつくる角のうち、小さい方の角は何度でしょう。
5時ぴったりのとき、長針と短針の間の角度は150°です。
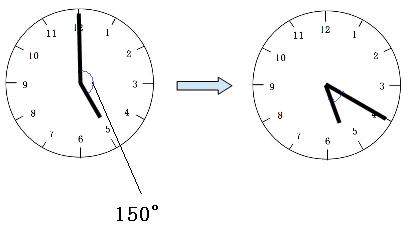
1分間で長針は短針に5.5°ずつ追いつくので、20分では、
5.5°×20分=110°
110°追いついたことになります。もともと150°だったものが110°追いついたので、5時20分のときの長針と短針の間の角は、
150°-110°=40°
よって答えは
40°
スポンサーリンク
(基本問題2)2時24分のとき、長針と短針がつくる角のうち、小さい方の角は何度でしょう。
2時ぴったりのとき、長針と短針の間の角度は60°です。
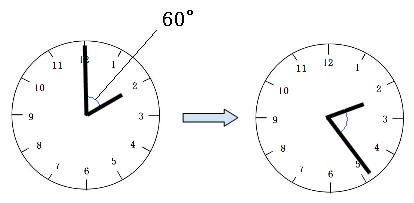
1分間で長針は短針に5.5°ずつ追いつくので、24分では、
5.5°×24分=132°
132°追いついたことになります。もともとは60°しかありませんでした。
つまり、まず60°分追いついて、そのあと72°分追いこしたということになります。一応式にしておくと、
132°-60°=72°
よって答えは
72°
(基本問題3)9時5分のとき、長針と短針がつくる角のうち、小さい方の角は何度でしょう。
9時ぴったりのとき、長針と短針の間の角度は90°です。

1分間で長針は短針から5.5°ずつ離れていくので、5分では、
5.5°×5分=27.5°
27.5°離れたことになります。もともとは90°だったので、
90°+27.5°=117.5°
よって答えは
117.5°
(基本問題4)8時32分のとき、長針と短針がつくる角のうち、小さい方の角は何度でしょう。
8時ぴったりのとき、長針と短針の間の角度は240°です。
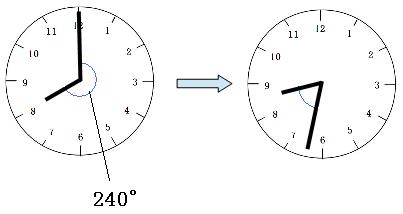
1分間で長針は短針に5.5°ずつ追いつくので、32分では、
5.5°×32分=176°
176°追いついたことになります。もともとは240°だったので、
240°-176°=64°
よって答えは
64°
(基本問題5)午後2時から午後5時の間に、長針と短針が直角になるのは何回あるでしょう。
午後2時ぴったりのとき、長針と短針の間の角度は60°です。
この状態から頭の中で時計を進めていき、長針と短針が直角になるのが何回あるか考えていきます。正確な時間を求める必要はありません。
難しければ、時計の絵を描きながらゆっくり考えましょう。

よって答えは
5回
頭の中で時計の針をグルグル回していると、なんだかグルグルしてきますね。
スポンサーリンク
エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!
保護者向けの人気記事
転塾を考えるときにやるべき3つのこと
成績が上がらなければ塾を変えるべきか。塾の内部を知る講師からの目線で、失敗しない塾の選び方のコツを紹介しています。
【中学受験】スタサプの2つのデメリットを克服する方法
スタサプで成績を上げるために必要なことを解説します。
子どもが勉強したがらない!勉強のやる気アップのポイントはたった1つだけ
勉強のやる気アップのポイントを解説します。(note記事)
中学受験のための算数塾が電子書籍になりました!
超基本から難関中学過去問に挑戦できるレベルへ!20年以上塾で教えてきた著者が「速さって何だろう?」という根本から丁寧に解説をします。
塾講師・先生向けの人気記事
初心者脱却!塾講師のための12のコツ
塾講師の本質的なテクニック!20年以上塾で教えてきた著者が、塾講師として必ず知っておいてほしいコツを12個にまとめました。
【塾講師・教室長向け】三者面談を失敗させない4つのポイント
塾講師や教室長が三者面談を行う時のコツと、売上げをアップさせるために必要な事を解説します。(note記事)
【失敗回避】塾講師をするなら集団授業か個別授業か
集団授業の塾講師になるメリットとデメリット、個別授業の塾講師になるメリットとデメリットを解説します。
ブラック企業でブラックバイト塾講師を雇ってた話
私がブラック企業の個人指導塾で教室長として働いていた時に、ブラックバイト講師を雇っていた時の話をします。















