流水算の練習問題③ 応用編
流水算の応用問題
こちらは、流水算の応用問題を載せているページです。
流水算の詳しい解説はこちら、基本問題はこちら、標準問題はこちらへどうぞ。
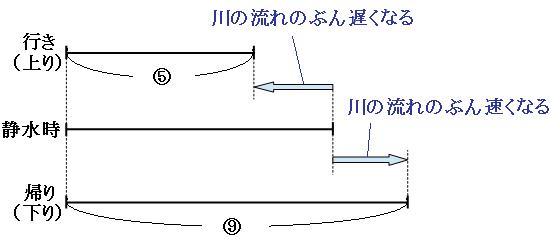
川を上る時は、川の流れの速さのぶん船は遅くなります。川を下る時は、川の流れの速さのぶん船は速くなります。
行きにかかった時間と、帰りにかかった時間の比は、
63分:35分=9:5
行きも帰りも道のりは同じなので、速さの比は時間の比の逆比になります。(速さと比の解説はこちら)
よって、行きの速さと帰りの速さの比は5:9。これを線分図に表すと、
この線分図のように、船の静水時の速さは、上りの時の速さと下りの時の速さのちょうど真ん中です。よって静水時の速さは、
(⑤+⑨)÷2=⑦
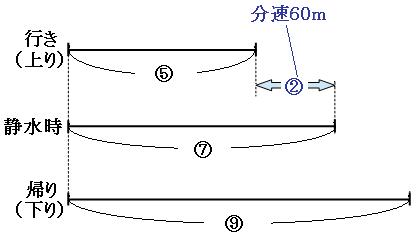
先ほどの線分図に、川の流れの速さが分速60mであることも書き込むと、
川の流れの部分の割合は、
⑦-⑤=②
②が分速60mにあたるので、①は分速30mです。
行きの速さは⑤なので、
分速30m×⑤=分速150m
行きにかかった時間は63分だったので、道のりは、
分速150m×63分=9450m
よって答えは
9450m
(1)川の流れの速さは分速何mでしょう。
(2)おばあさんがA地点を出発してから8分後に、B地点から桃が川に流されました。おばあさんと桃がすれ違うのは、おばあさんがA地点を出発してから何分後でしょう。 また、おばあさんが桃を追いこすのは、おばあさんがA地点を出発してから何分後でしょう。
(1)川の流れの速さは分速何mでしょう。
グラフを見て、おばあさんが川を上った時の速さと、下った時の速さを求めます。
上り
1200m÷12分=分速100m
下り
1200m÷4分=分速300m
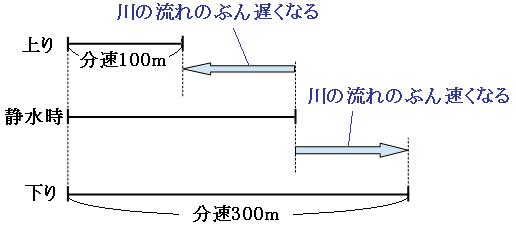
よって、静水時の速さ-川の流れの速さ=分速100m、静水時の速さ+川の流れの速さ=分速300mであることがわかりました。線分図を書いて、川の流れの速さを求めます。
線分図より、おばあさんの静水時の速さは、
(分速100m+分速300m)÷2=分速200m
なので、川の流れの速さは、
分速300m-分速200m=分速100m
よって答えは
分速100m
(2)おばあさんがA地点を出発してから8分後に、B地点から桃が川に流されました。おばあさんと桃がすれ違うのは、おばあさんがA地点を出発してから何分後でしょう。 また、おばあさんが桃を追いこすのは、おばあさんがA地点を出発してから何分後でしょう。
まずは、桃の様子をグラフに書きこんでみましょう。桃は川の流れの速さ(分速100m)で下ってきますので、A地点に到着するまでの時間は、
1200m÷分速100m=12分
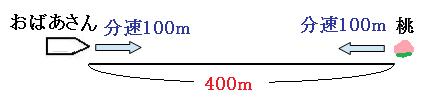
おばあさんがA地点を出発してから8分後の状況を考えます。おばあさんが8分間に進んだ道のりは、
分速100m×8分=800m
なので、B地点まではあと400mの地点にいます。
ここからは旅人算です。(旅人算の解き方はこちら)
おばあさんは1分間に100m、桃は1分間に100m進むので、1分間で縮まる道のりは、
100m+100m=200m
400mを縮めるのにかかる時間は、
400m÷200m=2
で、2分。最初の8分間もプラスして、
8分+2分=10分
次に、おばあさんがA地点を出発してから12分後(おばあさんがB地点い到着して、折り返してきた時)の状況を考えます。桃はすでに4分間流れていますので、その間に進んだ道のりは、
分速100m×4分=400m
おばあさんは1分間に300m、桃は1分間に100m進むので、1分間で縮まる道のりは、
300m-100m=200m
400mを縮めるのにかかる時間は、
400m÷200m=2分
で、2分。はじめの12分もプラスして、
12分+2分=14分
よって答えは
すれ違う…10分後
追いつく…14分後
「グラフを見ればわかるじゃん!」っていうツッコミは勘弁してください。今回は計算が大変にならないように分かりやすい数字を使ったので、グラフも分かりやすいところで交わってしまいました。 「グラフを見ても全然わからないよ!」という時のために、ちゃんと計算して求めています。(言い訳)
まずは、船が川を上る時の速さを求めます。
6000m÷30分=分速200m
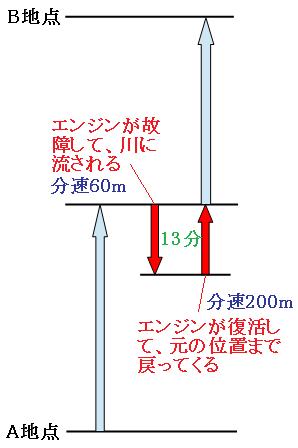
普段は30分で到着するのに、この日は43分かかっています。つまり、この日は普段よりも13分多く時間がかかっています。この13分は、エンジンが故障したために川に流されはじめてから、エンジンが復活して元の位置に戻ってくるまでの時間です。
この13分の間、エンジンが故障していたのが何分間で、エンジンが復活して元の位置に戻ってくるまでが何分間なのかを求めていきます。
まずは、川の流れの速さと、船が川を上る時の速さの比を求めます。
分速60m:分速200m=3:10
川に流された道のりと、元の位置に戻ってくるまでの道のりは同じなので、時間の比は速さの比の逆比になります。(速さと比の解説はこちら)
よって、エンジンが故障していた時間と、エンジンが復活して元の位置まで戻ってくる時間の比は10:3。
つまり、エンジンが故障していた時間は、13分を10:3に分けたうちの10の方になります。
13分÷(10+3)×10=10分
よって答えは
10分
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!