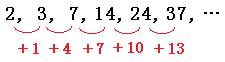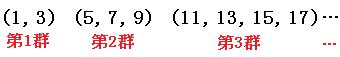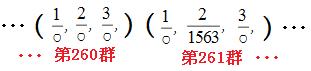数列の練習問題③　応用編

（応用問題1）あるきまりにしたがって、整数が次のように並んでいます。

2, 3, 7, 14, 24, 37, ・・・


（1）47番目の数はいくつでしょう。

（2）100番目の数はいくつでしょう。

（1）47番目の数はいくつでしょう。

この数列は階差数列です。

上の図のように、次の項へはいくつ足しているだろうと考えたら、「1, 4, 7, 10, ・・・」と、初めの数が1、公差が3の等差数列が現れました。 これをもとにして、それぞれの項を求めていきます。まずは第1項から第4項までの求め方を考えてみましょう。

第1項＝2
第2項＝2＋1＝3
第3項＝2＋1＋4＝7
第3項＝2＋1＋4＋7＝14
第4項＝2＋1＋4＋7＋10＝24

同じように考えると第47項は、

2＋1＋4＋7＋10＋13＋・・・

と、表すことができます。

初めの2だけは別ですが、その後の「1, 4, 7, 10,・・・」は等差数列ですので、公式を使って和を求めることができます。公式を使うためには、最後の数と、項の数を求めなければなりません。 「2, 3, 7, 14, 24, 37, ・・・」の数列の47番目の数を求めるので、「1, 4, 7, 10,・・・」の数列の項の数は46です。これは植木算の考え方で求められます。（植木算の解き方はこちら）

それでは、「1, 4, 7, 10, ・・・」の数列の、46番目の数を求めます。

第N項＝初めの数＋公差×（N－1）
＝1＋3×（46－1）
＝1＋3×45
＝1＋135
＝136

よって、最後の数は136です。それでは、「2, 3, 7, 14, 24, 37, ・・・」の数列の、47番目の数を求めます。

2＋1＋4＋7＋10＋13＋・・・＋136
＝2＋（1＋136）×46÷2
＝2＋137×46÷2
＝2＋3151
＝3153

よって答えは

3153

（応用問題2）あるきまりにしたがって、整数が次のように並んでいます。

（1）第21群の5個目の数はいくつでしょう。

（2）1001は、第何群の何個目の数でしょう。

（3）第15群の数をすべて足すといくつになるでしょう。

（1）第21群の5個目の数はいくつでしょう。

このように、規則正しくグループに分けてある数列を群数列といいます。 群数列は、それぞれの群の最後の数が、初めから数えて第何項目になるのかを考えるとよいです。

これを式に表してみると、

第1群の最後＝2項目
第2群の最後＝2＋3＝5項目
第3群の最後＝2＋3＋4＝9項目
第○群の最後＝2＋3＋4＋5＋・・・

つまり、第○群の最後の数が第何項なのかを求めるには、初めの数が2、公差が1の等差数列の和を求めればよいということがわかります。 さて、今回は第21群の5個目の数を求めるので、まずは第20群の最後の数が、初めから数えて何個目の数なのかを求めましょう。第20群にはいくつの数字が入っているでしょうか。
「第1群には2個」、「第2群には3個」、「第3群には4個」数字が入っていることから、「第20群には21個」数字が入っていることがわかります。 これらのことから第20群の最後の数は、初めから数えて何個目の数かというと、

2＋3＋4＋・・・＋21
＝（2＋21）×20÷2
＝23×20÷2
＝230

第20群の最後の数が、初めから数えて230個目の数ということがわかりました。 今回求める第21群の5個目の数は、初めから数えて「230個＋5個」で、235個目にあたります。

それでは、初めから数えて235番目の数がいくつなのかを考えてみましょう。この数列は「1. 3. 5. 7. 9. ・・・」と、初めの数が1、公差が2の等差数列です。その第235項は、

第N項＝初めの数＋公差×（N－1）
＝1＋2×（235－1）
＝1＋2×234
＝1＋468
＝469

よって答えは

469

（2）1001は、第何群の何個目の数でしょう。

1001が、初めから数えて何個目の数かを求めましょう。

初めの数＋公差×（N－1）＝第N項
1＋2×（N－1）＝1001
2×（N－1）＝1001－1
2×（N－1）＝1000
N－1＝1000÷2
N－1＝500
N＝501 （□や文字を求める計算の解き方）

ということで、1001は第501項目です。 先ほど、第20群の最後の数が第230項であることを求めました、第501項目はもう少し先になりそうです。試しに、第30群の最後の数が第何項目なのかを求めてみましょう。

第30群の最後＝2＋3＋4＋・・・＋31
＝（2＋31）×30÷2
＝33×30÷2
＝495

ラッキー！良い数字が出ました。第30群の最後の数は第495項となるので、今求めようとしている第501項は、第31群の中にあります。では、第31群の何個目の数かというと、

501－495＝6

より、6個目です。

よって答えは

第31群の6個目

（応用問題3）あるきまりにしたがって、整数が次のように並んでいます。

	1	,	2	,	3	,	1	,	2	,	3	,	1	, ・・・
	1		3		5		7		9		11		13

（1）分母が1563のとき、分子はいくつになるでしょう。

（2）1000番目の数はいくつでしょう。

（1）分母が1563のとき、分子はいくつになるでしょう。

分子が「1, 2, 3, 1, 2, 3, 1, 2, ・・・」と、規則正しく並んでいるので「1, 2, 3」を一組にしてグループに分けてしまいましょう。つまり、これは群数列です。

分母は「1, 3, 5, 7, 9, ・・・」と、初めの数が1、公差が2の等差数列になっています。分母が1563になるのは何番目の数か、公式を使って求めます。

初めの数＋公差×（N－1）＝第N項
1＋2×（N－1）＝1563
2×（N－1）＝1563－1
2×（N－1）＝1562
N－1＝1562÷2
N－1＝781
N＝782
（□や文字を求める計算の解き方）

よって、分母が1563になるのは、782番目の数です。ひとつの群には3つの分数が入っているので、3で割ってみます。

782÷3＝260あまり2

群が260個できて、分数が2つ余ります。つまり、分母が1563になる数は、第261群の2つ目の数です。よって分子は2。

よって答えは

2