速さと比の解き方
速さの比、道のりの比、時間の比
いつも通っている学校まで、いつもの2倍の速さで走ったら、いつもの半分の時間で到着します。 このように、速さと時間には反比例の関係があります。同じようにして、時間と道のりや、速さと道のりにも特別な関係があります。
- 道のりが同じとき
速さの比=a:bならば、時間の比=b:a
(速さが2倍なら、かかる時間は半分) - 時間が同じとき
速さの比=a:bならば、道のりの比=a:b
(速さが2倍で同じ時間走れば、進む道のりも2倍) - 速さが同じとき
道のりの比=a:bならば、時間の比=a:b
(同じ速さで走っているとき、道のりが2倍になれば、かかる時間も2倍)
どの関係にも「○○のとき」という条件がついているので、問題を解くときは必ず確認して下さい。 公式として覚えてしまってもよいですが、「速さが速くなれば(数字が大きくなれば)、時間は逆に短くなる(数字が小さくなる)。」のようにイメージして考えると楽だと思います。
速さと比の基本問題の解き方
それでは、実際に問題を解いてみます。
まずは、ウサイン・ボルト選手と烏丸先生が走った時間の比を求めてみましょう。
9.6秒:16.8秒=96:168
=4:7
ですので、ウサイン・ボルト選手と烏丸先生の速さの比は「7:4」。
よって答えは
7:4
出発してから出会うまでに、ふたりが歩いた時間は同じです。(違う時間に出会うにはタイムマシーンが必要です。)
時間が同じならば、速さの比と道のりの比は同じになります。[速さが速ければ(数字が大きければ)、同じように道のりも長い(数字が大きい)]
ですので、アリスが歩いた道のりと、カレンが歩いた道のりの比は「3:4」です。
カレンが歩いた道のりは、1400mを3:4に分けたうちの④の方なので、
1400m÷(③+④)×④
=800
(比の計算の解き方)
800m
「道のり」「速さ」「時間」のどれが同じなのかを見つけるようにするとひらめきやすいと思います。
それでは、速さのと比の基本をまとめます。
次は、速さの比を利用して問題を解いていきます。
速さと比の利用
ここまでで学習した速さの比、道のりの比、時間の比を利用すると、具体的な数字がわからなくても速さの問題を解くことができます。 ここでは、速さの比を利用して解く問題をいくつか紹介します。
速さと比の問題の解き方
道のりや速さの具体的な数字が分かっていなくて、道のり、速さ、時間のうち、ひとつでも同じものがあれば、速さと比を利用する可能性が高いです。
ふたりとも、家から学校まで同じ道のりを歩くことになるので、道のりは同じです。
具体的な歩いた時間はわからないのですが、歩いた道のりが同じなので、「速さと比の関係を使うのかな。」と思ってください。
まずは、ふたりが歩いた時間の差を求めてみましょう。
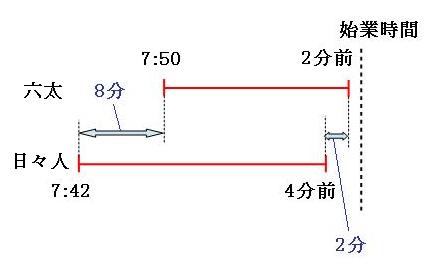
図のように、日々人の方が六太よりも8分早く家を出て、2分早く学校に着くので、
8分-2分=6分
で、日々人の方が6分多く歩いたことがわかります。
続いて、時間の比を求めます。まずは、六太と日々人の速さの比を出してみましょう。
分速80m:分速60m=4:3
ふたりが歩いた道のりは同じなので、速さと時間は逆比になります。
なので、六太が歩いた時間と日々人が歩いた時間の比は3:4になります。
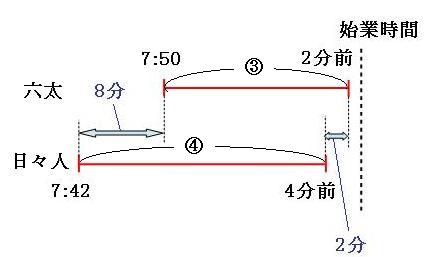
ふたりが歩いた時間の差が6分であることも含めて、時間の図にしてみます。
上の図の青い矢印の部分に注目します。この部分の比と時間は、
比→④-③=①
時間→6分
六太は③歩いて、到着の2分後に始業時間なので、六太が出発してから始業時間までの時間は、
6分×③+2分=20分
六太は7時50分に家を出ているので、始業時間は、
7時50分+20分=8時10分
よって答えは
8時10分
似た問題をもうひとつ。
例題3と同じ手順でも解けますが、出発時間が同じで、道のりを求めるときは、もうひとつ便利な解き方があります。
早く学校に着いた方は、普通は教室へ向かうのですが、このパターンの問題の場合は、遅れて到着する方が学校に着くまでそのまま真っ直ぐ歩き続けることにします。
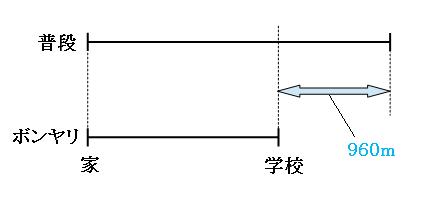
今回の問題では、普段の響が学校に着いたあとも、ボンヤリ響が学校に着くまでの12分間、真っ直ぐ歩き続けることにします。
この12分間に進める道のりは、
分速80m×12分=960m
また、普段の響も、ボンヤリ響が学校に到着するまで歩き続けたので、どちらも歩いた時間は同じです。
時間が同じなので、速さの比と道のりの比は同じになります。
よって、普段の響が歩いた道のりと、ボンヤリ響が歩いた道のりの比は、
80:50=8:5
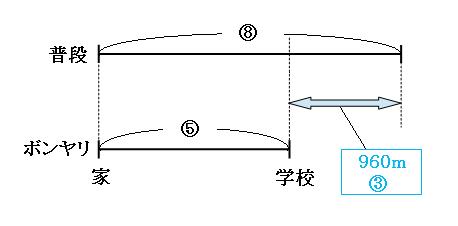
これをさっきの図に書き加えると、
上の図の青い矢印の部分に注目すると、
比→⑧-⑤=③
道のり→960m
より、③が960mに当たることがわかりました。①を求めるために、3で割ります。
960m÷③=320m
なので、①は320mです。線分図を見ると、家から学校までの道のりは⑤なので、
320m×⑤=1600m
よって答えは
1600m
例題3の手順で、歩いた時間を求めてから道のりを出しても大丈夫ですが、こっちの方が楽なので是非!
速さの比をそのまま「みはじ」の公式に使う
体積と比のときと同じように、本当の数字がわかっていなくても、比の数字をそのまま「みはじ」の公式に入れて使うことができます。
考え方は追いかける旅人算と同じです。(旅人算の解き方はこちら)
具体的な速さが出ていないので、比の数字を使って考えます。
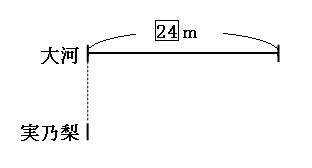
大河さんの速さを秒速②m、実乃梨さんの速さを秒速③mとします。本当の速さではないので、数字を○で囲ってあります。
まずは、実乃梨さんが追いかけ始めるまでに、大河さんが走った道のりを求めましょう。
秒速②m×12秒=24m
本当の道のりではないので、数字を□で囲ってあります。
追いかける旅人算なので、1秒後の状況を考えます。大河さんは1秒間に2m、実乃梨さんは1秒間に3m進みます。
よって、実乃梨さんが1秒間で縮められる距離は、
3m-2m=1m
ふたりの距離の差は24mあったので、この差を埋めるためにかかる時間は、
24m÷1m=24
よって答えは
24秒
友達が飛び出していってしまってから、追いかけると決めるまでの12秒間、きっと激しい葛藤があったのでしょう。
それでは、速さと比の利用をまとめます。
次は、歩幅と歩数のお話です。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!