時計算の解き方
時計算とは
時計算とは、時計の短針と長針の進み方を考え、針が重なる時の時刻や、短針と長針が特定の角度になる時の時刻を求めたり、逆に特定の時刻の短針と長針の間の角度を求めたりする問題です。 「短針と長針が重なる時刻なんて簡単じゃん!3時15分とかじゃん!!」って思ったりもするのですが、実は3時15分の時には短針は真っ直ぐ「3」の所を指しておらず、少し進んでしまっています。 時間とともに短針も動くので、2つの針の動きを同時に考えなければならなくて、こんがらがってしまったりします。
時計の針は1分で何度進む?
短針と長針が、それぞれ1分間にどれだけ回るか考えてみます。まずは長針に注目してみましょう。
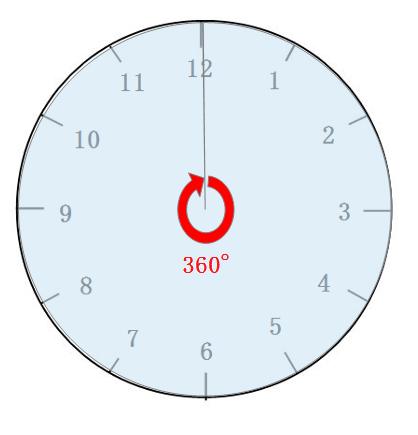
長針は1時間(60分)で360°回ります。
なので、5分間では、
360°÷12=30°
で、30°回ります。同じように考えると1分間では、
360°÷60分=6°
で、6°回ります。
それでは、短針はどうでしょうか。
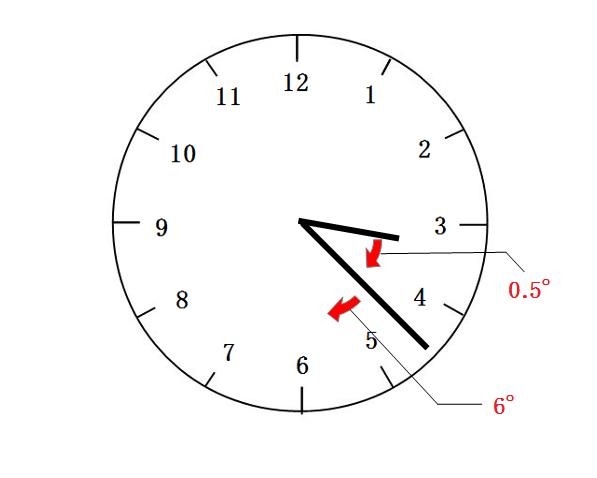
図のように、短針は1時間(60分)で30°回ります。よって1分では、
30°÷60分=0.5°
で、0.5°回ります。
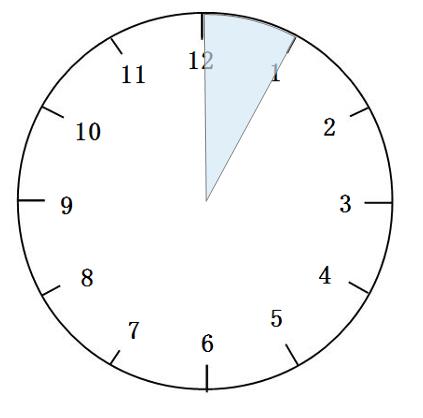
ここで、例えば3時ぴったりから、3時1分になるまでの針の動きを考えてみましょう。
図のように、1分間で長針が6°、短針が0.5°進むので、長針が短針に6°-0.5°=5.5°追いついたことになります。長針が短針を追い越した後も同じように考えると、
1分間で、長針が短針を5.5°ずつ引きはなしていきます。ここまでをまとめてみましょう。
続いて、実際に時計算の問題を解いていきます。
時計算の解き方
それでは、長針と短針の進み方をもとに時計算を解いていきましょう。 特に、「長針が短針に追いつくまでは、1分間に5.5°ずつ追いついていく」と、「長針が短針を追いこしたあとは、1分間に5.5°ずつはなれていく」を使って考えていきます。 コツは、3時00分や9時00分などのピッタリの時間の状況と、最後の状況をしっかりと考えることです。途中でわり算が出てきますが、時計の問題のわり算はわり切れないことが多いので、分数で答えるのが基本です。
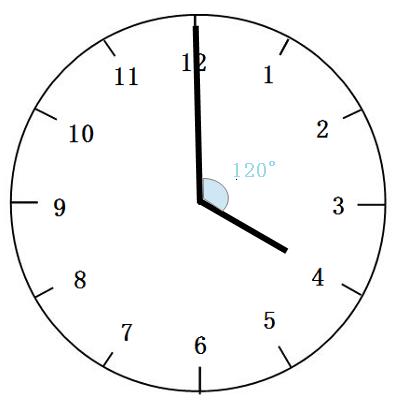
まずは4時00分ピッタリの時の時計の針を見てみましょう。
図のように、4時00分ピッタリの時点で、短針と長針の間は120°あります。続いて、短針と長針がぴったり重なった時の時計の針を見てみましょう。
図のように、短針と長針の間の角度は0°になりました。4時00分から、短針と長針がぴったり重なるまでの間に、長針は短針に120°追いついたことになります。 1分間で長針は短針に5.5°ずつ追いついていくので、120°追いつくために必要な時間は、
| 120°÷5.5° | = | 120÷ | 55 | |
| 10 |
| = | 120÷ | 11 | ||
| 2 |
| = | 120× | 2 | ||
| 11 |
| = | 240 | ||
| 11 |
| = | 21 | 9 | ||
| 11 |
| なので、4時21 | 9 | 分 | ||
| 11 |
| また、 | 9 | 分は、 | ||
| 11 |
1分(60秒)を11個に切ったうちの9個分なので、
| 60秒÷11×9 | = | 540 | ||
| 11 |
| = | 49 | 1 | ||
| 11 |
よって答えは
| 4時21分49 | 1 | 秒 | ||
| 11 |
分までしか出さない問題と、秒まで出す問題とがあります。単純な単位変換ですが、分数がブイブイ出てくるので間違えないようにしましょう。ちなみに時計算の場合は、
| 30° | = | 5 | 5 | 分 | ||
| 11 |
| 30° | = | 5分27 | 3 | 秒 | ||
| 11 |
と、覚えてしまう人もいます。ただし、「計算が苦手だから覚えてしまおう。」というのはおすすめしません。応用問題に対応できなくなります。覚えるのは「時計算の計算しすぎて、もう答え覚えちゃったよ!」っていう人だけにしましょう。
5時と6時の間で、長針と短針の間の角度が30°になるのは2回あります。
のときと、
のときです。①の場合から考えてみましょう。(例題1)と同じように、まずは5時00分ピッタリのときの長針と短針の状況を見てみましょう。
図のように、5時00分ピッタリの時点で、長針と短針の間は150°あります。続いて、長針と短針の間が30°になるとき①の状況をもう一度確認してみると、
なので、長針は短針に150°-30°=120°追いついたことになります。1分間で長針は短針に5.5°ずつ追いついていくので、120°追いつくために必要な時間は
| 120°÷5.5° | = | 120÷ | 55 | |
| 10 |
| = | 120÷ | 11 | ||
| 2 |
| = | 120× | 2 | ||
| 11 |
| = | 240 | ||
| 11 |
| = | 21 | 9 | ||
| 11 |
| なので、5時21 | 9 | 分 | ||
| 11 |
と、なります。続いて、長針と短針の間が30°になるとき②を考えてみましょう。5時00分ピッタリのときの状況が、
で、長針と短針の間は150°になっていて、長針が短針に追い付くと、
と、なります。この時点で短針は長針に150°追いついていますが、さらに時間が進んで長針と短針の間が30°になるとき②の状態になると、
となり、長針が短針をさらに30°追いこしたことになります。まとめると、長針は短針に150°追いつき、さらに30°追いこしたことになるので、全部で150°+30°=180°短針よりも多く進んだことになります。 1分間で長針は短針よりも5.5°多く進むので、
| 180°÷5.5° | = | 180÷ | 55 | |
| 10 |
| = | 180÷ | 11 | ||
| 2 |
| = | 180× | 2 | ||
| 11 |
| = | 360 | ||
| 11 |
| = | 32 | 8 | ||
| 11 |
| なので、5時32 | 8 | 分 | ||
| 11 |
よって答えは
| 5時21 | 9 | 分 | ||
| 11 |
| 5時32 | 8 | 分 | ||
| 11 |
長針と短針ふたつのことを考なくてはいけないと見せかけて、実は「1分間に5.5°」だけ考えれば良いというトリックです。それでは、時計算をまとめます。
計算頑張ってください。続いては、通過算の話に移ろうと思います。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!