水の中に立体を入れる問題
水の中に立体を入れるとき
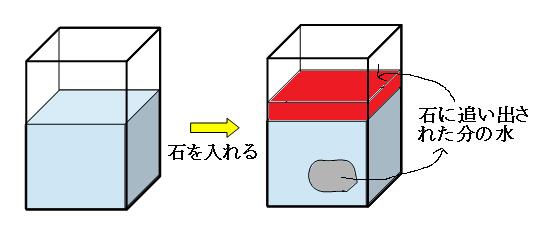
お風呂の中に入ると水面が上がるように(みんなで入るとあふれる!)、水の中に物を入れると、その物の体積の分だけ水が増えたように見えます。 この法則を使うと、体積を求める公式では求めることのできない、デコボコな石などの体積を測ることができます。
増えたように見える水の体積と、沈めた石の体積は同じです。
増えたように見える水の体積(上の図の赤い部分)の体積は、
10cm×10cm×2cm=200cm³
よって答えは
200cm³
水の中に立体を入れる問題の種類
水の中に立体を入れる問題は、大まかに分けて2種類のパターンがあります。
- 立体が完全に水の中に入っている
- 立体が水面から飛び出している
立体が完全に水の中に入っている問題の解き方
立体全体が水の中に入っている場合は、簡単に解くことができます。 先ほどのように、「増えたように見える水の体積=水に入れた立体の体積」の法則を使えば大丈夫です。
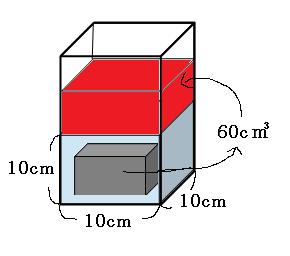
「増えたように見える水の体積=水に入れた立体の体積」です。
まずは、沈めた直方体の体積を出してみましょう。
3cm×5cm×4cm=60cm³
つまり、容器の中の水は60cm³増えたように見えます。
増えたように見える部分(上の図の赤いところ)に注目して、
深さ=体積÷底面の面積
=60cm³÷(10cm×10cm)
=6cm
もともと深さは10cmで、さらに6cm増えたので、全体の深さは16cm。
よって答えは
16cm
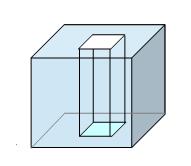
立体が水面から飛び出している問題の解き方
立体が水面から飛び出している場合は、先ほどとは全然違う方法で考えていきます。 立体が立っている部分には水はないので、その部分に穴が空いた状態と考えて解いていきます。
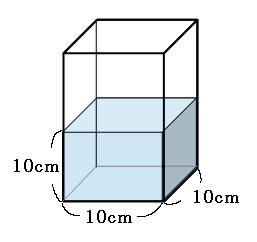
まずは、直方体を入れる前の状況を考えてみましょう。
容器に入っている水の体積は、
10cm×10cm×10cm=1000cm³
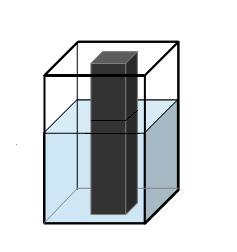
続いて、直方体を水の中に入れてみます。
上の図の水の部分だけ取り出すと、
このように、真ん中に穴が空いた直方体になります。
この図形が何角柱だか名前はわかりませんが、とにかく真っ直ぐ立っているの「柱」です。
柱の体積は、「底面の面積×高さ」で求めることができます。なので、水の深さは「体積÷底面の面積」で求められます。まずは底面の面積を求めましょう。
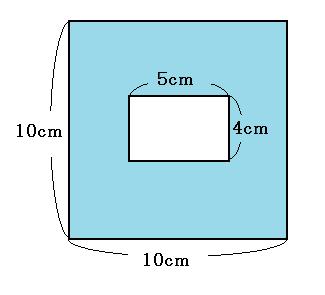
上の図の色がついている部分が底面になるので、その面積を求めると、
10cm×10cm-4cm×5cm
=100cm²-20cm²
=80cm²
なお、実際には水の体積は増えても減ってもいないので、最初の状態と変わりません。
つまり、1000cm³のままです。だから、
水の深さ=体積÷底面の面積
=1000cm³÷80cm²
=12.5cm
12.5cm
「水の中に立体を入れる」という似たような問題なのに、立体が全て水に入っているか、水面から「こんにちは!」しているかで、全然別の視点から解いていくことになります。
2パターンをしっかりと練習しましょう。
それでは、水の中に立体を入れる問題をまとめます。
ここまでで体積は終わりです。次は、比を使った速さの問題を解きます。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!