流水算の練習問題② 標準編
流水算の標準問題
こちらは、流水算の標準問題を載せているページです。
流水算の詳しい解説はこちら、基本問題はこちら、応用問題はこちらへどうぞ。
川を上る時は、川の流れの速さのぶん船は遅くなります。川を下る時は、川の流れの速さのぶん船は速くなります。
（標準問題1）静水時の速さが150mの船があります。
この船が川を1200m下るのに6分かかります。川を1200m上るのには何分かかるでしょう。
川を下る話から、川の流れの速さを求めていきます。1200mを6分で下ったので、その速さは
1200m÷6分＝分速200m
川を下っているので、川の流れの速さのぶん船は速くなっています。静水時の速さは分速150mだったので、川の流れの速さは、
分速200m－分速150m＝分速50m
より、川の流れの速さは分速50mです。これを使って、川を上った時の話を考えていきましょう。
川を上る時は、川の流れのぶん船は遅くなりますので、船の速さは、
分速150m－分速50m＝分速100m
分速100mで1200m進むので、かかる時間は、
1200m÷分速100m＝12分
よって答えは
12分
スポンサーリンク
（標準問題2）ある船が、川を4620m上るのに33分、下るのに21分かかりました。
この船の静水時の速さは分速何mでしょう。また、川の流れの速さは分速何mでしょう。
まずは、川を上る時と下る時の船の速さを求めます。
上り
4620m÷33分＝分速140m
下り
4620m÷21分＝分速220m
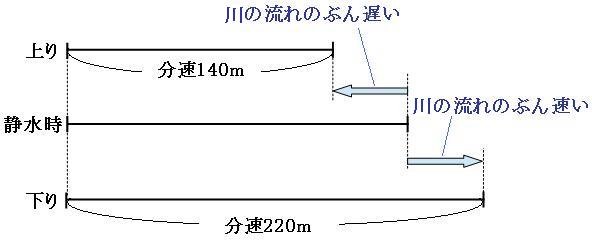
川の流れの速さのぶん遅くなると分速140m、川の流れの速さのぶん速くなると分速220mです。線分図にして表してみます。
この線分図のように、船の静水時の速さは、上りの時の速さとと下りの時の速さのちょうど真ん中です。よって静水時の速さは、
（分速140m＋分速220m）÷2＝分速180m
船の静水時の速さが分速180mなので、川の流れの速さは、
分速180m－分速140m＝分速40m
よって答えは
船の静水時の速さ…分速180m
川の流れの速さ…分速40m
（標準問題3）静水時の速さが時速16kmの船があります。
この船が、ある川の上流と下流の2地点を往復するのに、行きは3時間、帰りは5時間かかりました。この川の流れの速さは時速何kmでしょう。
行きにかかる時間と帰りにかかる時間の比は3:5です。行きも帰りも道のりは同じなので、速さの比は逆比になります。
行きの速さ:帰りの速さ＝5:3
（速さと比の解説はこちら）
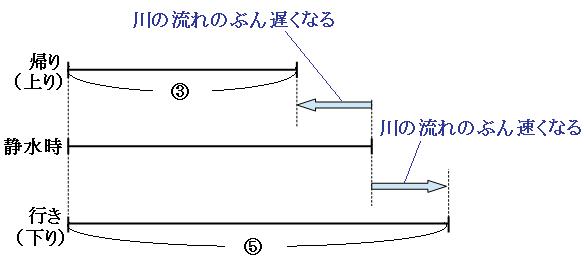
これを線分図で表してみると、
この線分図のように、船の静水時の速さは、上りの時の速さと下りの時の速さのちょうど真ん中です。よって静水時の速さは、
（③＋⑤）÷2＝④
船の静水時の速さが時速16kmでした。先ほどの④と一緒に線分図に書き込むと、
線分図より、④が時速16kmにあたるので、①を求めると、
時速16km÷④＝時速4km
よって、①が時速4kmにあたります。行き（下り）の速さは⑤なので、
時速4km×⑤＝時速20km
船の静水時の速さが時速16km、川を下る時の速さが時速20kmなので、川の流れの速さは、
時速20km－時速16km＝時速4km
よって答えは
時速4km
スポンサーリンク
エデュサポオリジナル受験生応援グッズ販売中！
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生！！
保護者向けの人気記事
転塾を考えるときにやるべき3つのこと
成績が上がらなければ塾を変えるべきか。塾の内部を知る講師からの目線で、失敗しない塾の選び方のコツを紹介しています。
【中学受験】スタサプの2つのデメリットを克服する方法
スタサプで成績を上げるために必要なことを解説します。
子どもが勉強したがらない！勉強のやる気アップのポイントはたった1つだけ
勉強のやる気アップのポイントを解説します。(note記事)
中学受験のための算数塾が電子書籍になりました！
超基本から難関中学過去問に挑戦できるレベルへ！20年以上塾で教えてきた著者が「速さって何だろう？」という根本から丁寧に解説をします。
塾講師・先生向けの人気記事
初心者脱却！塾講師のための12のコツ
塾講師の本質的なテクニック！20年以上塾で教えてきた著者が、塾講師として必ず知っておいてほしいコツを12個にまとめました。
【塾講師・教室長向け】三者面談を失敗させない4つのポイント
塾講師や教室長が三者面談を行う時のコツと、売上げをアップさせるために必要な事を解説します。(note記事)
【失敗回避】塾講師をするなら集団授業か個別授業か
集団授業の塾講師になるメリットとデメリット、個別授業の塾講師になるメリットとデメリットを解説します。
ブラック企業でブラックバイト塾講師を雇ってた話
私がブラック企業の個人指導塾で教室長として働いていた時に、ブラックバイト講師を雇っていた時の話をします。
