旅人算の練習問題② 標準編
旅人算の標準問題
こちらは、旅人算の標準問題を載せているページです。
旅人算の詳しい解説はこちら、基本問題はこちら、応用問題はこちらへどうぞ。
まずは、日向が折り返し地点に着いた時のことを考えましょう。日向が折り返し地点に着くまでの時間は、
3100m÷分速310m=10分
10分間に影山が走った道のりは、
分速290m×10分=2900m
つまり、スタートから10分後、日向は折り返し地点にいて、影山はあと200mで折り返し地点という場所にいます。図に表すと、
2人は逆向きに進んでいて、日向は1分間に310m進み、影山は1分間に290m進みます。その和は600mなので、出会うまでにかかる時間は、
| 200m÷600m | = | 200 | |
| 600 |
| = | 1 | ||
| 3 |
| 1 | 分= | 1 | ×60秒 | ||
| 3 | 3 |
=20秒
日向が折り返し地点に着くまでの10分も合わせて、
10分+20秒=10分20秒
よって答えは
10分20秒後
まだ追いつけます!頑張れ影山!
2人は逆方向に進んでいます。
まずは、1分間に進む2人の道のりの合計を考えます。4分後にすれ違ったということは、4分間で2人合わせて1800m進んだということです。つまり1分間では、
1800m÷4分=450m
自分は1分間で250m進むので、おじさんが1分間に進んだ道のりは、
450m-250m=200m
よって答えは
分速200m
いつもの考え方の逆ですね!
2人は同じ方向に進んでいます。
ハーバートが家を出るまでに、ジョージはすでに10分歩いています。その間に歩いた道のりは、
分速60m×10分=600m
ということで、ハーバートが家を出る時点で、2人は600m離れていることがわかりました。
ジョンは1分間に60m、ハーバートは1分間に180m進むので、1分間に縮まる2人の道のりは、
180m-60m=120m
よって、ハーバートはジョンに追いつくまでにかかる時間は、
600m÷120m=5
で、5分です。ハーバートがジョンに追いつくと同時にホワイトハウスに到着するので、結局、ハーバートは家からホワイトハウスまで5分かかったということになります。その間に走った道のりは、
分速180m×5分=900m
よって答えは
900m
このままでは計算が大変なので、速さの単位を秒速mに換えます。
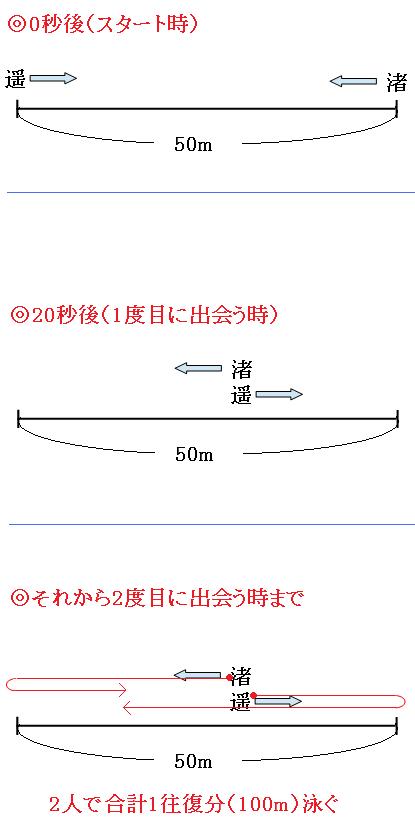
遥
分速90m÷60=秒速1.5m
渚
分速60m÷60=秒速1m
遥は1秒間に1.5m、渚は1秒間に1m進むので、
50m÷(1.5m+1m)
=50m÷2.5m
=20
より、20秒で出会うことが分かりました。
次に出会うまでに、2人が泳ぐそれぞれの道のりは分からないのですが、合計ならば分かります。プール1往復分、100mです。
なので、次に出会うまでにかかる時間は、
100m÷(1.5m+1m)
=100m÷2.5m
=40
で、40秒です。1度目に出会うまでの20秒も合わせて、
40秒+20秒=60秒
よって答えは
60秒
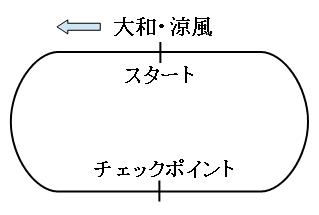
まずは、大和が涼風に追いつくまでの時間を求めましょう。2人は同じ方向に進んでいます。
大和は1分間に250m、涼風は1分間に210m進むので、追いつくまでにかかる時間は、
400m÷(250m-210m)
=400m÷40m
=10
で、10分です。つまり、この10分間にチェックポイントを何回通過したかを考えればokです。
まずは、大和が10分間で何周するか求めます。10分間で大和が走る道のりは、
分速250m×10分=2500m
1周400mなので、
2500m÷400=6あまり100
6週と100m走ったことになります。スタートからチェックポイントまでは200mありますので、最後の7週目はチェックポイントまで届いていません。よって、大和は6回チェックポイントを通過しています。
涼風も同じように考えると、
(分速210m×10分)÷400m
=5あまり100m
よって、涼風は5回チェックポイントを通過しています。なので2人合わせると、
6回+5回=11回よって答えは
11回
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!