体積と比
水の容積と底面積と深さの比
容器の中に入っている水などの体積を「容積」といいます。
柱の容器に入れた水の容積が同じならば、底面の面積と深さは逆比になるという法則があります。
柱の容器に入っている水の容積が同じ時
底面の面積の比＝a:bならば、
深さの比＝b:a
容器に入っている水の体積は同じなので、底面の面積と深さは逆比になります。
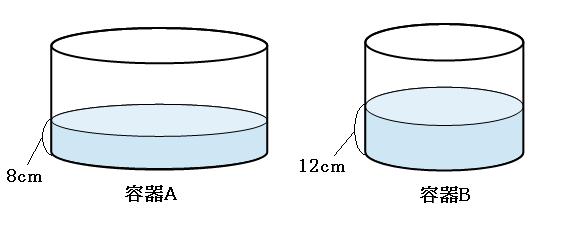
今回は深さの比＝8cm:12cmなので、
底面の面積の比＝12:8
＝3:2
よって答えは
3:2
底面積の比と深さの比で、容積の比を求める
柱の体積の公式を使って、そのまま容積の比を求めることができます。
柱の体積＝底面の面積×高さ
容積の比＝底面の面積の比×高さの比
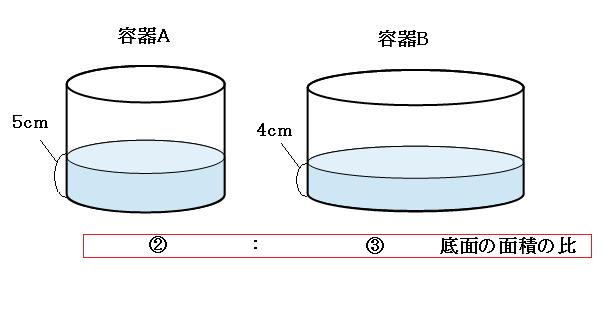
「容積の比＝底面の面積の比×高さの比」なので、容器Aと容器Bに入っている水の体積の比は、
（②×5cm）:（③×4cm）＝10:12
＝5:6
よって答えは
5:6
同じ深さにする容積の問題の解き方
容積の比は、いろいろな問題で活用できます。特によく問われるのは、いくつかの容器の水の深さを同じにする問題です。
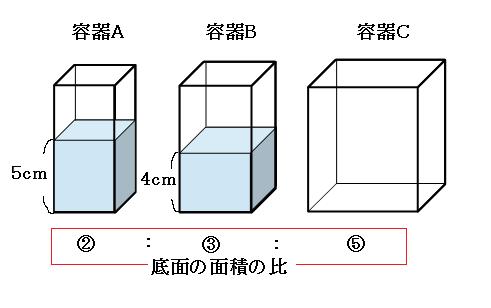
実際の底面の面積がいくつなのかわからないのですが、ここでは比の数字をそのまま使って、それぞれ②、③、⑤としてしまいます。
体積の求め方は「底面積×高さ」なので、これを使って水の体積を求めていきます。
容器A
②×5cm＝10
容器B
③×4cm＝12
10＋12＝22
よって、水の体積は全部で22です。
底面の本当の面積がわかっていないので、22という数字は本当の体積ではありません。なので□で囲っておきました。単位も書きません。
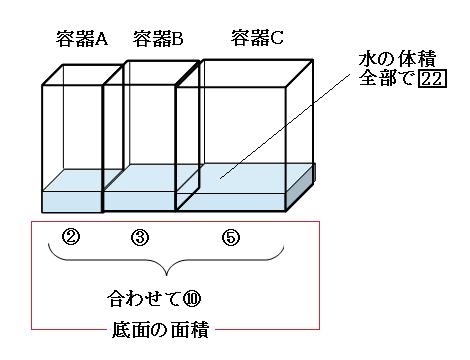
続けてこの水を容器Cに移すわけなのですが、「水を移す」と考えるよりも、「3つの容器を合体させる」と考えた方がわかりやすいと思います。
というわけで、合体させてみます。
合体させると底面の面積は、
②＋③＋⑤＝⑩
水の体積は先ほど22と求めたので、
水の深さ＝水の体積÷底面の面積
＝22÷⑩
＝2.2
よって答えは
2.2cm
このように、本当の面積や、本当の長さでなくても、比の数字を使って体積の公式にあてはめることができます。
この考え方は速さや面積など、いろいろな場面で使うことができるのですが、使ってもいいのかダメなのかの判断が少し難しいので、まずはこの「深さを同じにする問題」をたくさん解いて、感覚をつかんでおきましょう。
それでは体積と比をまとめます。
次は容器を傾けてみます。
