面積図を使った速さの問題

速さの問題に面積図を使う

面積図は「たて×横＝面積」の公式を使っているので、かけ算を使うものとは基本的に相性が良いです。速さの公式にも「速さ×時間＝道のり」という公式があるので、面積図を使って考えることができます。が、速さの問題は、面積図を使わなくても解けてしまうことが多いので、あまり面積図の出番がありません。では、どんな時に面積図が便利かというと、途中で速さが変わり、それぞれの道のりと時間がわからない時です。途中で速さが変わっても、それぞれの道のりか時間が出ていれば面積図を使う必要はありません。

途中で速さが変わる問題の解き方

途中で速さが変わる速さの問題は、「それぞれの道のりはわからないけれども、合計の道のりはわかっている」ものが多いです。そうです、つるかめ算の考え方です。つるかめ算を理解していれば簡単に解けるでしょう。たてを速さ、横を時間、面積を道のりに置きかえます。

たて×よこ＝面積
速さ×時間＝道のり

速さの問題なので、速さの計算問題はできるようにしてから挑戦しましょう。

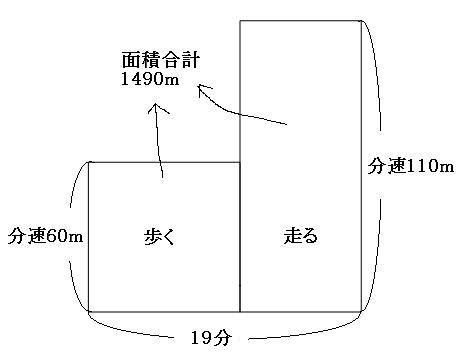
（例題1）朝7時40分に、家から学校へ向かって歩き始めました。はじめは分速60mの速さで歩いていたのですが、「このままでは遅刻遅刻！」と思ったので、途中から分速110mの速さで走ったら、7時59分に学校に着きました。家から学校までの道のりは1490mです。歩いた道のりと走った道のりは、それぞれ何mでしょう。

歩いた道のりと走った道のりそれぞれはわかりませんが、合計は1490mと書いてあります。この状況では面積図が便利です。

たて×よこ＝面積
速さ×時間＝道のり

さっそく面積図を書いていきます。朝7時40分に家を出て、7時59分に学校へ着いているので、家から学校まで19分かかっています。それぞれの時間はわからないので、横の長さは適当に書いておきます。

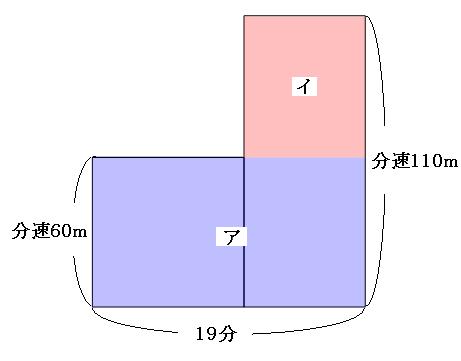
あとはつるかめ算の時の面積図の見方と同じです。この面積図を下の図のように分けてみます。

「ア」の部分の面積は、

分速60m×19分＝1140m

全体の面積が1490mだったので、残りの「イ」の部分の面積は、

1490m－1140m＝350m

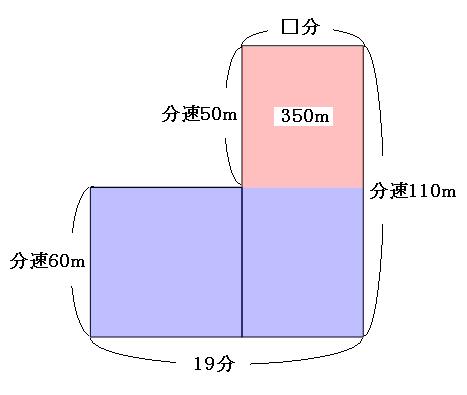
「イ」の部分の横の長さを□分として、もう一度「イ」の部分に注目してみます。

「イ」の部分の長方形のたての長さは、

分速110m－分速60m＝分速50m

よって、「イ」の長方形は、たてが分速50m、横が□分、面積が350mなので、

□＝350÷50＝7

で、横の長さが7分であることが求められました。「イ」の部分の横の長さは、走った時間を表していたので、走った時間は7分。全部で19分かかっていたので、

19分－7分＝12分

で、歩いた時間は12分であることがわかりました。あとは、それぞれの道のりを求めていきます。

速さ×時間＝道のり
歩き→分速60m×12分＝720m
走り→分速110m×7分＝770m

よって答えは

歩いた道のり…720m、走った道のり…770m

「ちこくちこく～！」と言いながら走ると、曲がり角で人にぶつかることがあるので気をつけましょう。
速さの問題を苦手とする人が多く、しかも途中で速さが変わってしまうなんてチンブンカンブンって思われがちなのですが、面積図を書いてしまえば、途中から長方形の面積の問題になってしまうので簡単です。それでは、途中で速さが変わる速さの問題をまとめます。

まとめ

途中で速さが変わり、それぞれの道のりと時間がわからない速さの問題を解くときは