表面積① 角柱や円柱の表面積
表面積の基本
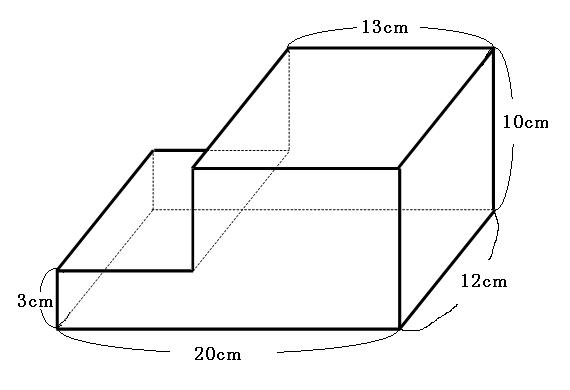
表面積とは、立体の表面の面積を全て合わせた面積です。基本的には、ひとつひとつの面の面積を地道に求めて足していきます。
はじめに、立体には面がいくつあって、どんな形になっているかを整理してから計算を始めると、間違いが少なくなりますよ!
ひたすら面積を求めますので、面積の公式を頭に叩き込んでおいてください。(面積の公式はこちら)
基本の表面積の求め方
「円」と名のつくものが出てこなければ、簡単な問題が多いです。
ただ、計算が多いのでミスをしやすいです。
はじめに、面の形をよく見て、工夫できるところはないか考えてから計算を始めた方が良いです。
地道に全ての面の面積を足せばOKです。今回は少しだけ工夫をしてみます。
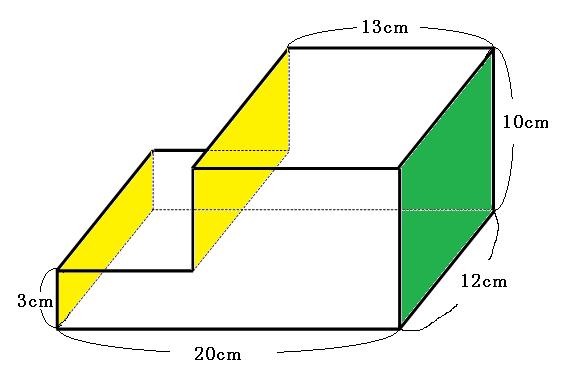
上の図の黄色の長方形を合体させると、緑色の長方形と同じになります。同じようにして、
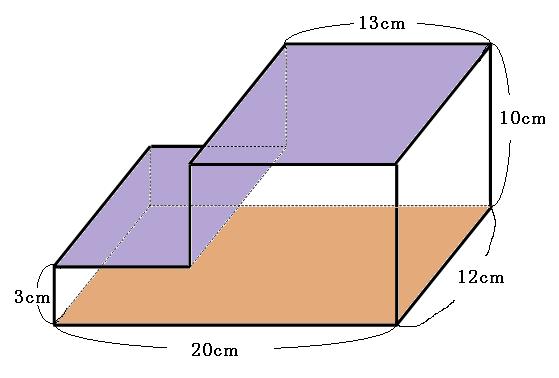
上の図の紫の長方形を合体させると、茶色の長方形と同じになります。(図が見づらくてすいません。)
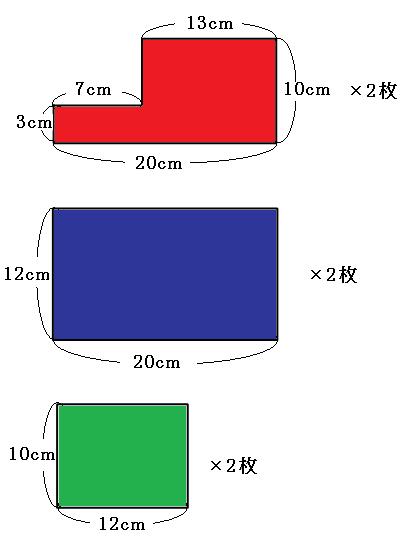
なので、求める面積をまとめると、
上の図のようになります。合計6枚です。では、面積を求めていきましょう。
(3×7+10×13+12×20+10×12)×2
=(21+130+240+120)×2
=511×2
=1022
よって答えは
1022cm²
円柱の表面積の求め方
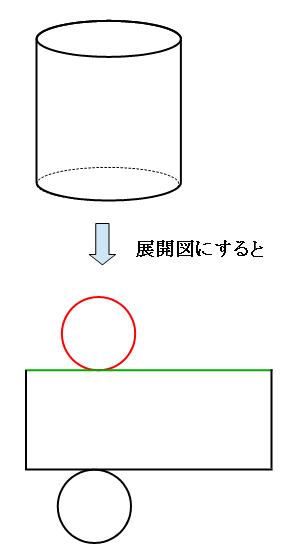
円柱の表面積を求めるときは、展開図を書いて考えます。円柱の展開図は、円と長方形になります。
円柱の表面積を求めるときに一番困ってしまうのは、長方形の部分の横の長さが分からないことです。
が、底面の円周(上の図の赤い部分)と、側面を開いた長方形の横の部分(上の図の緑の部分)は、もともと同じ所だったので、長さは同じです。
ここだけ気をつけていれば、円柱の表面積も簡単に求められます。
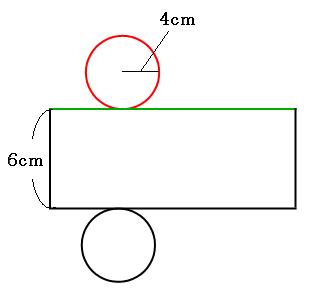
まずは展開図を書きます。
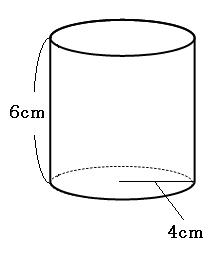
上の図の赤い部分と緑の部分の長さは同じです。赤い部分は半径4cmの円の円周なので、その長さは、
4cm×2×3.14=25.12cm
なので、緑の部分も25.12cmです。
求める表面積は、円が2つと長方形が1つなので、
4×4×3.14×2+6×25.12=251.2
よって答えは
251.2cm²
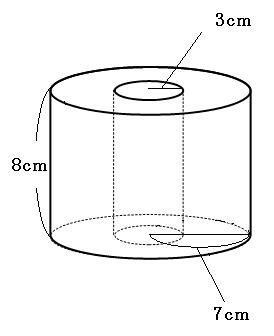
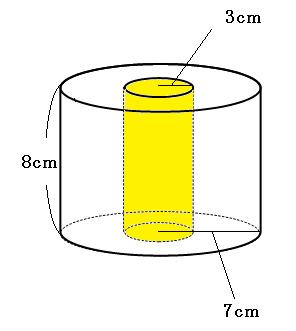
求める面積は4ヶ所です。ドーナツのような底面が2枚、一番外側の側面が1枚、内側が1枚。特にくり抜かれている内側の部分を忘れやすいので気をつけてください。
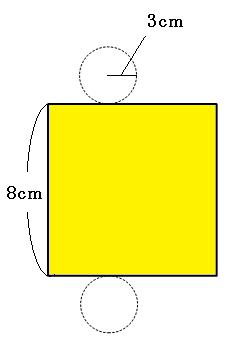
まずはくり抜かれている内側(上の図の黄色の部分)の面積を考えます。円柱の側面になっているので、展開図を書きます。
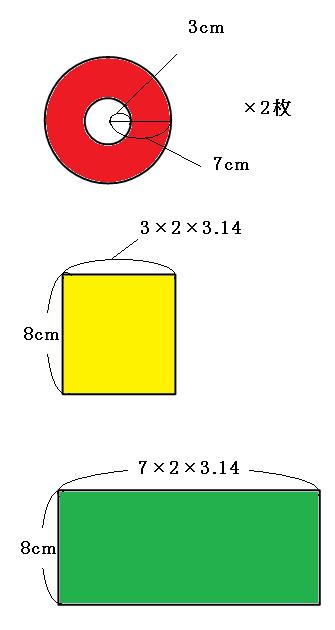
上の図の黄色い長方形の横の長さは、3×2×3.14。
同じように考えて、一番外側の側面の横の長さは、7×2×3.14
ここまでをまとめて、求める4ヶ所の面積を考えます。
計算していきましょう。なるべくひとつの式にまとめると、途中計算が楽になります(サボれます)。
(7×7×3.14-3×3×3.14)×2+
8×3×2×3.14+8×7×2×3.14
=49×2×3.14-9×2×3.14+48×3.14+112×3.14
=(98-18+48+112)×3.14
=240×3.14
=753.6
よって答えは
753.6cm²
特に円柱の表面積は3.14の計算が多くなりますので、計算をサボる方法を一生懸命考えてください。
それでは、角柱と円柱の表面積をまとめます。
次は、円錐の表面積を求めます。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!