図形の回転移動
図形の回転移動とは
回転移動とは、図形が、形を変えることなく、ある点を中心にして一定の角度だけ回転することです。
ただ、中学受験の算数では、ほとんどが頂点を中心にして回転移動をしたり、床の上を図形がゴロゴロ転がったりするパターンが多いです。
回ったり転がったりするので、おうぎ形が登場します。おうぎ形の弧の長さの求め方と、面積の求め方を思い出しておきましょう。

図形の回転移動の問題の解き方
コツは、移動とともに、図形はどのように動いたのかを頭の中でしっかり想像することです。
点の移動や、図形の平行移動よりは想像しやすいと思います。
回転するので、「円やおうぎ形になるな。」と意識していれば大丈夫だと思います。
想像したら、その線や形を図に書きこんでおくと問題が解きやすいですよ!
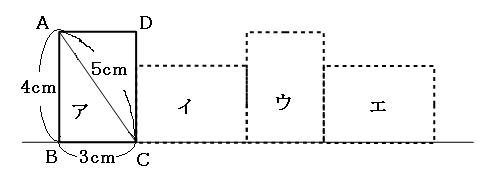
(1)アの位置からエの位置まで移動するまでに、頂点Aが移動した距離は何cmでしょう。
(2)アの位置からイの位置まで移動するまでに、線分ACが移動したあとの面積は何cm²でしょう。
(1)アの位置からエの位置まで移動するまでに、頂点Aが移動した距離は何cmでしょう。
まず最初に、長方形の頂点はどの頂点も90°なので、どの回転も90°回転していることを頭に入れておいてください。
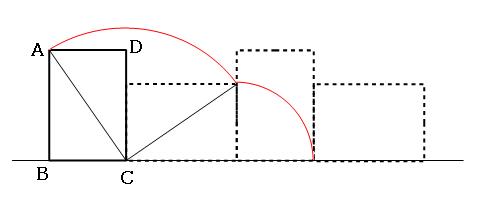
それでは頂点Aがどのように移動したか考えてみましょう。
上の図の赤い線が、頂点Aが移動したあとです。ウの位置からエの位置に回転するときは、頂点Aは動きません。
おうぎ形がふたつ見えれば、あとは計算をするだけです。
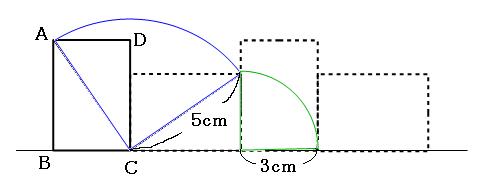
青いおうぎ形の弧の長さと、緑のおうぎ形の弧の長さを足します。どの回転も90°回転しているので、どちらのおうぎ形も中心角は90°です。
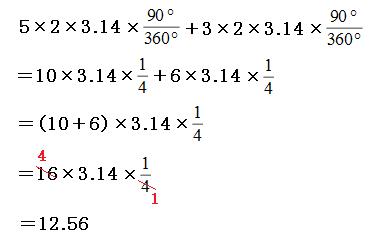
よって答えは
12.56cm
(2)アの位置からイの位置まで移動するまでに、線分ACが移動したあとの面積は何cm²でしょう。
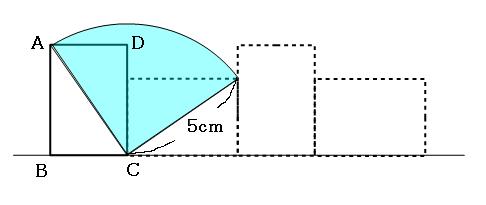
まずは、線分ACがどのように移動したか考えてみましょう。
線分ACが移動したあとは、上の図のような水色のおうぎ形になります。あとは計算をして面積を求めるだけです。
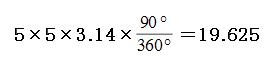
よって答えは
19.625cm²
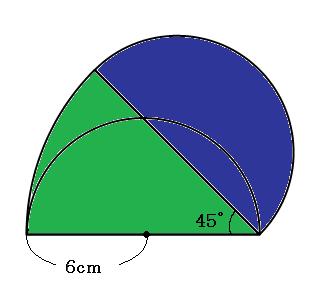
どこから求めれば良いのか、少し迷ってしまう図形なのですが、よくよく見てみればきっと簡単です。
まずは、ポッカリと空いてしまっている半円の部分もふくめて、面積を求めます。
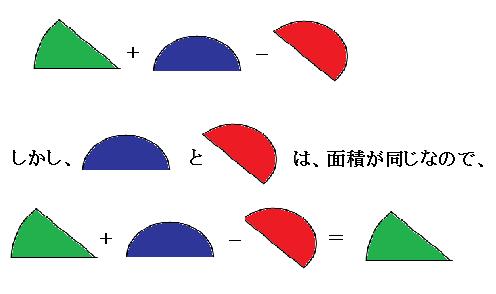
全体の面積は、緑のおうぎ形の面積と、青の半円の面積を足した分です。そして、ここからポッカリ空いた半円を引きます。
まとめると、
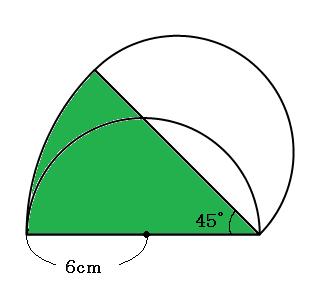
つまり、緑のおうぎ形の部分の面積だけを求めればokです。45°回転移動しているので、このおうぎ型の中心角は45°です。
よって答えは
56.52cm²
回転移動の問題というより、おうぎ形の面積を求める問題という感じがします。
円やおうぎ形の問題は、3.14のかけ算が出てくるので、計算をする前に「何か工夫できるところはないかな?(サボれるところないかな?)」と、少し考えてみてください。
それでは、図形の回転移動の問題をまとめます。
次は、図形の周上を円が転がるお話です。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!