ニュートン算の練習問題② 応用編
ニュートン算の応用問題
こちらは、ニュートン算の応用問題を載せているページです。
ニュートン算の詳しい解説はこちら、標準問題はこちらへどうぞ。
ニュートン算のポイントは、行列のはじめの状況が分かっている時は1分後のことを考え、行列の始めの状況が分かっていない時は線分図を書くことです。
行列(水槽)の最初の状況が分からないので、線分図を書いて考えます。
1分間に①Lの水が流入してくるとして、水がなくなるまでに流入してきた水の量と、ポンプが排水した水の量を考えましょう。
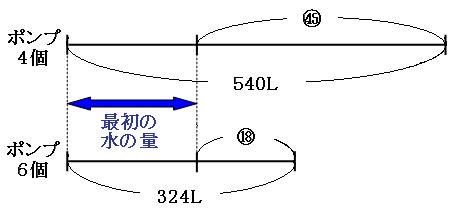
◎ポンプ4個で45分かかる場合
流入した水
①×45分=㊺
ポンプが排水した水の量
3L×4個×45分=540L
◎ポンプ6個で18分かかる場合
流入した水
①×18分=⑱
ポンプが排水した水の量
3L×6個×18分=324L
これらをもとに、線分図を書いていきます。
この線分図を見比べると、
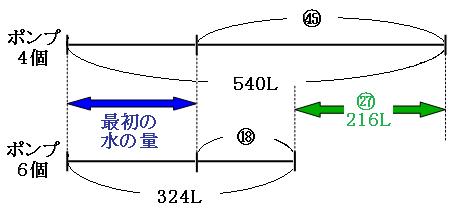
線分図の緑の矢印の部分に注目すると、
割合
㊺-⑱=㉗
水のかさ
540L-324L=216L
より、㉗が216Lにあたることが分かりました。これより①を求めると、
216L÷㉗=8L
線分図を見ると、最初に入っていた水の量は、
540L-㊺
=540L-8L×45
=180L
よって答えは
180L
(1)はじめの行列の人数は、1分間に2つのレジを通る人数の何倍でしょう。
(2)レジを3つ開けると、行列は何分でなくなるでしょう。
(1)はじめの行列の人数は、1分間に2つのレジを通る人数の何倍でしょう。
行列の最初の状況が分からないので、線分図を書いて考えましょう。
レジを通る人数は行列に増えていく人数の4倍なので、1分間に行列に増えていく人数を①人、レジを通る人数を④人とします。
それでは、行列がなくなるまでの10分間の状況を考えましょう。
行列に加わった人数
①×10分=⑩人
レジを通った人数
④×10分=㊵人
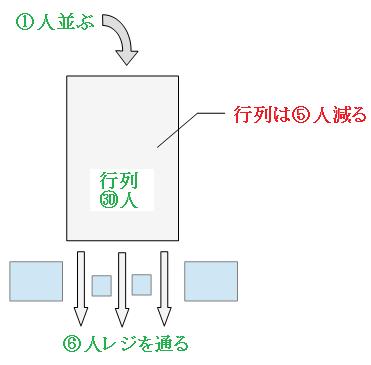
これを線分図に書いてみると、
上の線分図は、はじめの行列の人数から10分間で⑩人増えて、同じく10分間で㊵人減ると、行列が0人になることを表しています。この線分図より、はじめの行列の人数は、
㊵人-⑩人=㉚人
はじめの行列の人数が㉚人、1分間に2つのレジを通る人数が④人なので、
㉚人÷④人=7.5
よって答えは
7.5倍
(2)レジを3つ開けると、行列は何分でなくなるでしょう。
行列の最初の状況が分かっているので、1分後のことを考えましょう。
レジを2つ開けると、1分間に④人レジを通ります。今度はレジを3つ開けるので、1分間にレジを通る人数は、
④人÷2つ×3つ=⑥人
1分間で①人列に加わり、⑥人がレジを通っていくので、行列から減った人数は、
⑥人-①人=⑤人
よって、㉚人の行列がなくなるまでにかかる時間は、
㉚人÷⑤人=6
よって答えは
6分
まずは仕事算を使います。(仕事算の解説はこちら)
ひとつひとつの能力が違うので、仕事全体の量(水槽の容積)を①とします。
1分間にするそれぞれの管とせんの仕事を求めます。
A管
| ① | ÷ | 15分 | = | 1 | |
| 15 |
B管
| ① | ÷ | 10分 | = | 1 | |
| 10 |
A管+B管
| 1 | + | 1 | = | 1 | |
| 15 | 10 | 6 |
せん
| ① | ÷ | 10分 | = | 1 | |
| 10 |
ここからはニュートン算で考えます。
行列(水槽)の最初(せんがぬけてしまった時)の状況が分からないので、線分図を書いて考えましょう。
A管+B管が6分間に入れる水の量は、
| 1 | × | 6分 | = | 1 | |
| 6 |
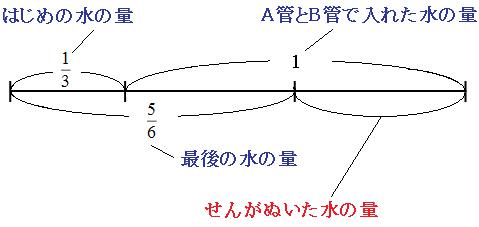
これをもとに線分図を書くと、
上の線分図より、せんによって捨てられた水の量は、
| 1 | + | 1 | - | 5 | = | 1 | |
| 3 | 6 | 2 |
この量の水をぬくのにかかる時間は、
| 1 | ÷ | 1 | = | 5 | |
| 2 | 10 |
で、5分かかります。6分間のうちの5分間はせんがぬけていたので、せんがぬけた時間は、
6分-5分=1分
よって答えは
1分後
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!