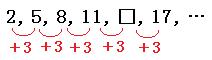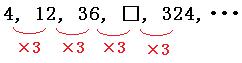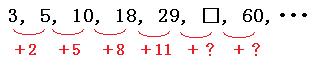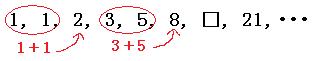数列の練習問題① 基礎編
数列の基本問題
こちらは、数列の基本問題を載せているページです。
数列の詳しい解説はこちら、標準問題はこちら、応用問題はこちらへどうぞ。
（基本問題1）次の数列の□に入る数字はいくつでしょう。
2, 5, 8, 11, □, 17, ・・・
2, 5, 8, 11, □, 17, ・・・
この数列は、初めの数が2、公差が3の等差数列です。
□に入る数字は、
11＋3＝14
よって答えは
14
スポンサーリンク
（基本問題2）次の数列の□に入る数字はいくつでしょう。
100, 94, 88, 82, □, 70, ・・・
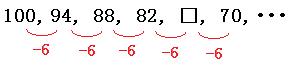
100, 94, 88, 82, □, 70, ・・・
この数列は、初めの数が100、公差が-6の等差数列です。
□に入る数字は、
82－6＝76
よって答えは
76
（基本問題3）次の数列の□に入る数字はいくつでしょう。
4, 12, 36, □, 324, ・・・
4, 12, 36, □, 324, ・・・
この数列は、初めの数が4、公比が3の等比数列です。
□に入る数字は、
36×3＝108
よって答えは
108
（基本問題4）次の数列の□に入る数字はいくつでしょう。
3, 5, 10, 18, 29, □, 60, ・・・
3, 5, 10, 18, 29, □, 60, ・・・
いくつ足すと次の項になるのかを見てみましょう。
「2, 5, 8, 11,・・・」と、初めの数が2、公差が3の等差数列が出てきたのが見えますでしょうか。
これで、「＋11」の次は「＋14」であることがわかります。
よって□に入る数字は、
29＋14＝43
よって答えは
43
（基本問題5）次の数列の□に入る数字はいくつでしょう。
| 1 | , | 2 | , | 3 | , | 4 | , | □ | , | 6 | , ・・・ | ||
| 3 | 5 | 7 | 11 |
| 最初の1は | 1 | なので、 | ||
| 1 |
| 1 | , | 2 | , | 3 | , | 4 | , | □ | , | 6 | ,・・・ | ||
| 1 | 3 | 5 | 7 | 11 |
分母と分子を別々に考えていきます。
分子は、初めの数が1、公差が1の等差数列で、分母は、初めの数が1、公差が2の等差数列です。
よって□に入る数字は、
分子
4＋1＝5
分母
7＋2＝9
よって答えは
5 9
（基本問題6）次の数列の□に入る数字はいくつでしょう。
1, 1, 2, 3, 5, 8, □, 21, ・・・
1, 1, 2, 3, 5, 8, □, 21, ・・・
この数列は、前の2つの数を足すと次の数になるフィボナッチ数列です。
□に入る数字は、
5＋8＝13
よって答えは
13
スポンサーリンク
- 受験生応援オリジナルグッズ
エデュサポオリジナル受験生応援グッズ販売中！
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生！！
