時計算の練習問題② 標準編
時計算の標準問題
こちらは、時計算の標準問題を載せているページです。
時計算の詳しい解説はこちら、基本問題はこちら、、応用問題はこちらへどうぞ。
時計算のポイントは、1分間で長針は短針に5.5°ずつ追いつく、またははなれていくことです。
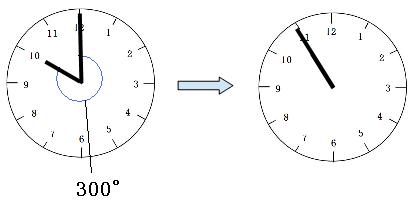
10時ぴったりのとき、長針と短針の間の角度は300°です。
1分間で長針は短針に5.5°ずつ追いつくので、300°追いつくのにかかる時間は、
| 300°÷5.5° | = | 300÷ | 11 | |
| 2 |
| = | 54 | 6 | ||
| 11 |
| また、 | 6 | 分を秒に直すと、 | ||
| 11 |
| 6 | ×60= | 32 | 8 | 秒 | ||
| 11 | 11 |
よって答えは
| 10時54分32 | 8 | 秒 | ||
| 11 |
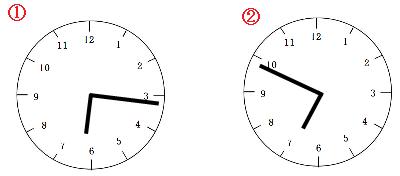
6時から7時の間で、長針と短針が直角になる時は2回あります。
6時ちょうどのとき、長針と短針の間の角度は180°です。
まずは①の方から考えてみましょう。①の状態になるには、長針は短針にあと90°追いつかなければなりません。
1分間で長針は短針を5.5°ずつ追いつくので、90°追いつくのにかかる時間は、
| 90°÷5.5° | = | 90÷ | 11 | |
| 2 |
| = | 16 | 4 | 分 | |||
| 11 |
続いて②の方も考えてみます。②の状態になるには、長針が短針に追いついて、さらに90°追いこさなければなりません。つまり全部で、
180°+90°=270°
で、270°追いこすことになります。 1分間で長針は短針を5.5°ずつ追いこすので、270°追いこすのにかかる時間は、
| 270°÷5.5° | = | 270÷ | 11 | |
| 2 |
| = | 49 | 1 | 分 | |||
| 11 |
よって答えは
| 6時16 | 4 | 分, | 6時49 | 1 | 分 | ||
| 11 | 11 |
答えを2つ求めなければならないことに気がつくことが重要です。
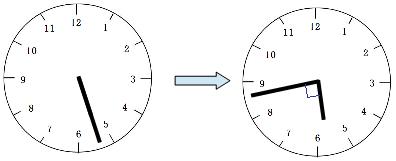
5時から6時の間で、長針と短針が重なるのは、5時25分~30分の間です。正確な時間を求める必要はありません。
長針と短針が重なっているとき、その間の角度は0°です。それが90°に広がりました。 1分間で長針と短針の間は5.5°ずつ広がっていくので、90°広がるのにかかる時間は、
| 90° ÷5.5° | = | 90÷ | 11 | |
| 2 |
| = | 16 | 4 | 分 | |||
| 11 |
よって答えは
| 16 | 4 | 分 | ||
| 11 |
(2)午前0時から午後11時59分までに、長針と短針は何回重なるでしょう。
(1)長針と短針が重なってから、次にもう一度重なるのは何分後でしょう。
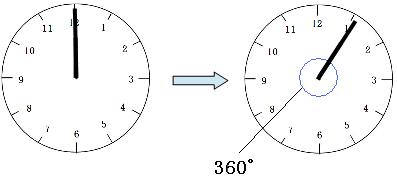
何時を基準にして考えても同じ答えが出るのですが、一番簡単なので12時ちょうどを基準として考えましょう。
12時ちょうどのとき、長針と短針の間の角度は0°です。次に重なるまでに(1時5分頃)、長針は短針を360°追いこさなければなりません。
1分間で長針は短針を5.5°ずつ追いこすので、360°追いこすのにかかる時間は、
| 360° ÷5.5° | = | 360÷ | 11 | |
| 2 |
| = | 65 | 5 | 分 | |||
| 11 |
よって答えは
| 65 | 5 | 分後 | ||
| 11 |
(2)午前0時から午後11時59分までに、長針と短針は何回重なるでしょう。
午前0時から午後11時59分までは、実際には23時間59分なのですが、計算が面倒なので24時間で計算してしまいます。24時間は、
24×60=1440
より、1440分です。

で、22回なのですが、最後の22回目は午前0時です。今回は午後11時59分までですので、この1回は引いいておきましょう。
また、今回の計算では一番最初の午前0を数えていません。植木算の考え方です。(植木算の解説はこちら)
なので、この1回を足しておきましょう。この2つのことも考えると、
22回-1回+1回=22回
よって答えは
22回
ひたすら5.5°です。このページで一体何回「5.5°」って書いただろうかというくらい5.5°です。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!