時計算の練習問題③ 応用編
時計算の応用問題
こちらは、時計算の応用問題を載せているページです。
時計算の詳しい解説はこちら、基本問題はこちら、時計算の標準問題はこちらへどうぞ。
時計算のポイントは、1分間で長針は短針に5.5°ずつ追いつく、またははなれていくことです。
1年は365日です。エリンの時計は1日で2秒遅れますので、1年間では、
2秒×365日=730秒
730÷60=12あまり10
で、12分10秒遅れます。よって、次の年の1月1日午前0時にエリンの時計が示している時刻は、
午前0時-12分10秒
=午後11時47分50秒
よって答えは
午後11時47分50秒
ちりも積もって山となりましたね!最近の時計は自動で時刻を合わせてくれるので、こういった心配もなくなりました。
短針は1分間に0.5°、長針は1分間に6°進むので、短針と長針の速さの比は、
0.5°:6°=1:12
(比の計算方法はこちら)
だから、4時ちょうどから、角Aと角Bが等しくなる時刻までに進んだ短針と長針の道のり(角度)も1:12になります。
(速さと比の解説はこちら)
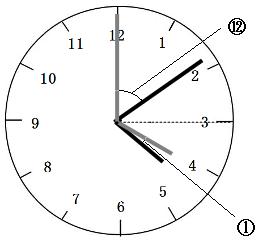
このことを考えて図に書きこんでみると、
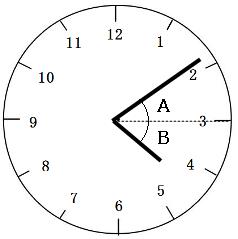
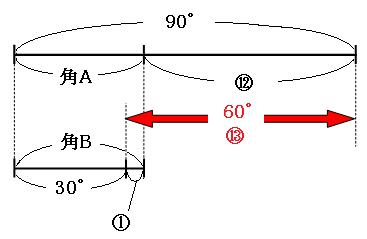
まずは、角Aに注目してみます。
4時ちょうどから4時15分まで進むと、長針は90°動きます。4時ちょうどから、角Aと角Bが等しくなる時刻までに長針は⑫動きましたので、
角A=90°-⑫
続いて、角Bに注目してみます。
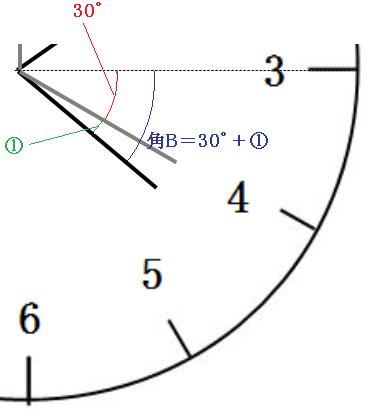
文字盤の「3」と「4」の間は30°です。4時ちょうどから、角Aと角Bが等しくなる時刻までに短針は①動きましたので、
角B=30°+①
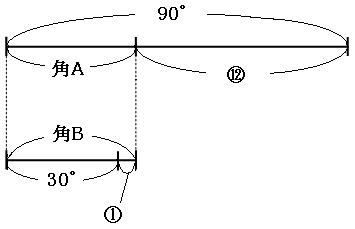
角Aと角Bが等しいことに注目して、倍数算の考え方で線分図を書いて考えます。
(倍数算の解説はこちら)
この線分図を見比べて、
⑬が60°に当たるので、①は、
| 60÷⑬ | = | 60 | |
| 13 |
| なので、①は | 60 | |
| 13 |
4時ちょうどから、角Aと角Bが等しくなる時刻までに短針は①動いてます。短針は1分間に0.5°進むので、短針が①動くのにかかる時間は、
| 60 | ÷0.5= | 120 | |
| 13 | 13 |
| = | 9 | 3 | ||
| 13 |
よって答えは
| 4時9 | 3 | 分 | ||
| 13 |
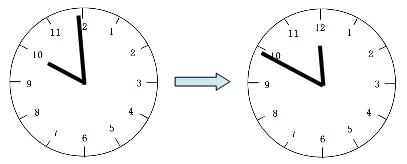
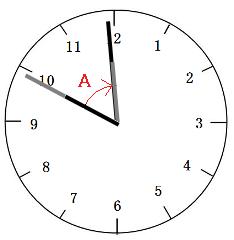
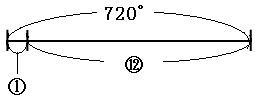
短針が進んだ角度は、下の図のAの部分です。
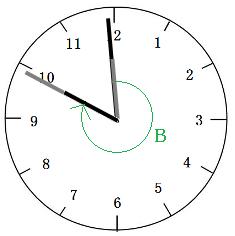
長針が進んだ角度は1周+下の図のBの部分です。
A+Bは、ちょうど1周分(360°)になります。
よって、メイがちょっとそこまで行っている間に、長針と短針が進んだ角度の合計は、
A+B+1周
=1周+1周
=2周
=720°
短針は1分間に0.5°、長針は1分間に6°進むので、短針と長針の速さの比は、
0.5°:6°=1:12
(比の計算方法はこちら)
だから、メイがちょっとそこまで行っている間に進んだ短針と長針の道のり(角度)も1:12になります。
(速さと比の解説はこちら)
ここまでまとめると、短針と長針が進んだ角度の合計は720°、短針と長針の進んだ角度の比は1:12。
上の図より、⑬が720°にあたるので、①は、

よって答えは

時計算は、結構派手な分数が出てきますよね!でも、分母の数はあまり種類が多くはありません。応用問題3の答えの「143」という分母も、よく見る数ですよ!
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!