倍数算の練習問題③ 応用編
倍数算の応用問題
こちらは、倍数算の応用問題を載せているページです。
倍数算の詳しい解説はこちら、基本問題はこちら、標準問題はこちらへどうぞ。
倍数算は線分図の読み取り方が特徴的です。しっかり練習してマスターしましょう!(線分図についてはこちら)
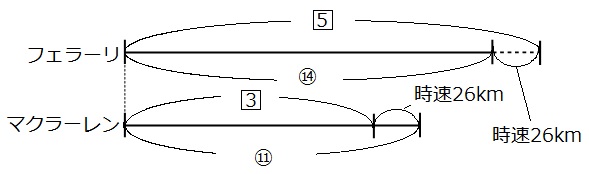
まずは線分図を書いてみましょう。
はじめの速さの差がわかりません。更に、どちらの線分図も長さが変わってしまっています。
このパターンの場合は、線分図を伸ばして、○か□の比の部分をの長さを同じにします。今回は□の数字を合わせます。
上の線分図を3倍、下の線分図を5倍に伸ばして、15で長さを合わせます。スペースの都合上、本当に伸ばしたものは書けません、ごめんなさい。
上の線分図(フェラーリの線分図)は、すべての数字が3倍になっています。同様に、下の線分図(マクラーレンの線分図)は、すべての数字が5倍になっています。
それでは、この線分図を見比べて、数字も割合もわかる部分を探してみましょう。
緑の矢印の部分に注目すると、
速さ
時速78km+時速130km=時速208km
割合
![]()
⑬が時速208kmにあたるので、①は、
時速208km÷⑬=時速16km
これで、①が時速16kmに当たることがわかりました。
ここで、最初に書いた線分図を見てみましょう。
フェラーリの車の最初の速さは、⑭よりも時速26km速いので、
時速16km×⑭+時速26km=時速250km
よって答えは
時速250km
伸ばした線分図は、見ているだけだと簡単そうに見えますが、自分で書いてみると意外と難しいです。コツは、始めに、合わせた数字のところの長さをそろえて書くことです。今回の問題ならば15の部分の線分図を最初に書いてしまうと書きやすいです。
また、①を求めた後に線分図を見る時は、最初に書いた線分図を見てください。伸ばしたあとの線分図を見てしまうと、間違った答えが出てしまいます。
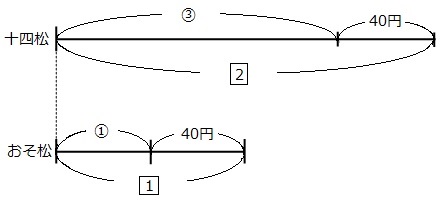
まずは線分図を書いてみましょう。
はじめのお金の差がわかりません。更に、どちらの線分図も長さが変わってしまっています。
このパターンの場合は、線分図を伸ばして、○か□の比の部分をの長さを同じにします。今回は□の数字を合わせます。
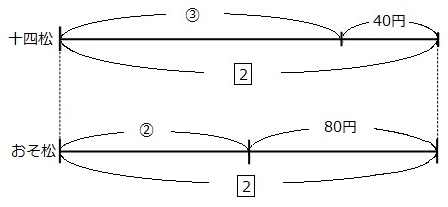
上の線分図(十四松)を1倍、下の線分図(おそ松)を2倍に伸ばして、2で長さを合わせます。
上の線分図(十四松の線分図)は、変化していません。下の線分図(おそ松の線分図)は、すべての数字が2倍になっています。
それでは、この線分図を見比べて、数字も割合もわかる部分を探してみましょう。
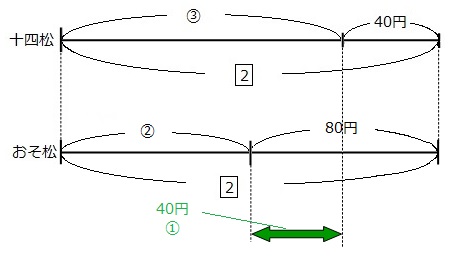
緑の矢印の部分に注目すると、
お金
80円-40円=40円
割合
③-②=①
これで、①が40円に当たることがわかりました。
ここで、最初に書いた線分図を見てみましょう。
十四松さんがはじめに持っていたお金は③、おそ松さんがはじめに持っていたお金は①なので、
十四松: 40円×③=120円
おそ松: 40円×①=40円
よって答えは
十四松:120円、おそ松:40円
線分図を伸ばして○か□の比の部分をの長さを同じにする際は、○と□どちらの数字を合わせても大丈夫です。
ただ、①がいくつなのかを知りたい時は、□の数字を合わせたほうが便利です。
同じように、1がいくつなのかを知りたい時は、○の数字を合わせたほうが便利です。
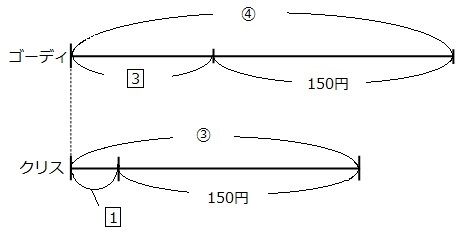
まずは線分図を書いてみましょう。
はじめに持っているお金の差がわかりません。更に、どちらの線分図も長さが変わってしまっています。
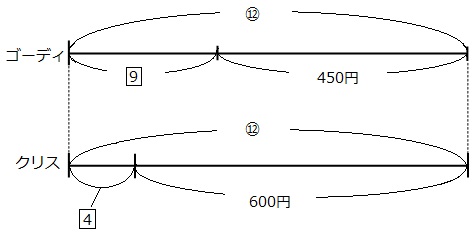
このパターンの場合は、線分図を伸ばして、○か□の比の部分をの長さを同じにします。今回は○の数字を合わせます。
上の線分図(ゴーディ)を3倍、下の線分図(クリス)を4倍に伸ばして、⑫で長さを合わせます。スペースの都合上、本当に伸ばしたものは書けません、ごめんなさい。
上の線分図(ゴーディの線分図)は、すべての数字が3倍になっています。同様に、下の線分図(クリスの線分図)は、すべての数字が4倍になっています。
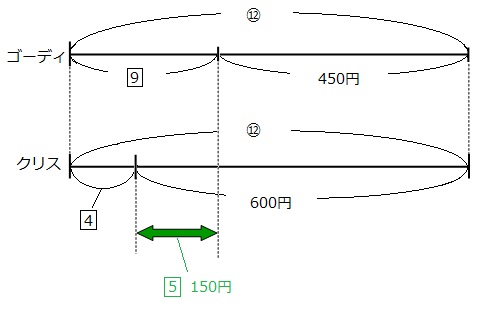
それでは、この線分図を見比べて、数字も割合もわかる部分を探してみましょう。
緑の矢印の部分に注目すると、
お金
600円-450円=150円
割合
9-4=5
5が150円にあたるので、1は、
150円÷5=30円
これで、1が30円に当たることがわかりました。
ここで、最初に書いた線分図を見てみましょう。
1つのチョコバーの値段は、
3+1=4
で、4に当たります。よって、1つのチョコバーの値段は、
30円×4=120円
よって答えは
120円
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!