倍数算の練習問題②　標準編

線分図を書いて見比べていきます。

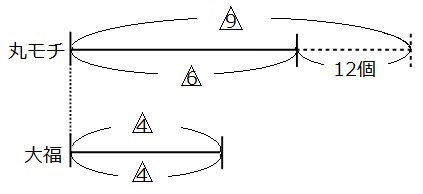
はじめのおモチの数の差はわかりません。大福の線分図の長さは変わっていません。ですので、大福の線分図の比の数字を最小公倍数でそろえます。 ④と2の最小公倍数は4です。○はそのまま（1倍）で、□は2倍しましょう。

○も□も、大福の線分図の部分が4になったので、同じ仲間として足し算や引き算ができるようになりました。
それでは線分図を見て、個数と比の両方がわかる部分を探しましょう。

よって答えは

36個

線分図を書いて見比べていきます。

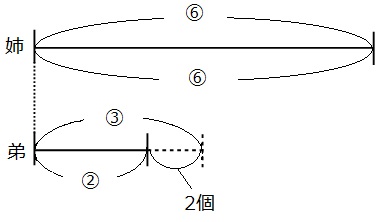
はじめのプリンの数の差はわかりません。姉の線分図の長さは変わっていません。ですので、姉の線分図の比の数字を最小公倍数でそろえます。 □を3倍、△を2倍して、線分図を書き直してみましょう。

□も△も、姉の線分図の部分が6になったので、同じ仲間として足し算や引き算ができるようになりました。
それでは線分図を見て、個数と比の両方がわかる部分を探しましょう。

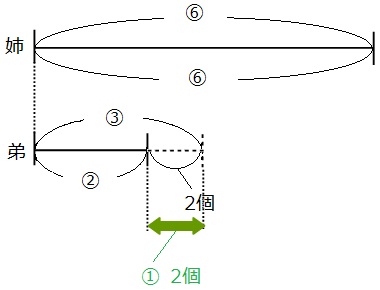
上の線分図の緑の矢印の部分に注目してみましょう。

比→③－②＝①
個数→2個

なので、①が2個に当たることがわかりました。姉が持っているプリンの数は⑥なので、

2個×⑥＝12個

よって答えは

12個

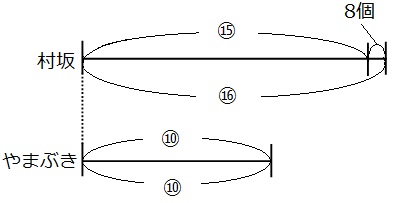
線分図を書いて見比べていきます。

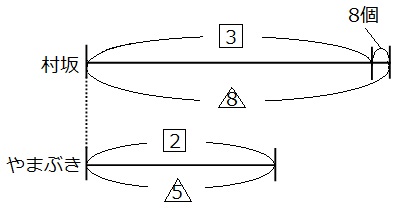
はじめのメロンパンの数の差はわかりません。やまぶきベーカリーの線分図の長さは変わっていません。ですので、やまぶきベーカリーの線分図の比の数字を最小公倍数でそろえます。 □を5倍、△を2倍して、線分図を書き直してみましょう。

□も△も、やまぶきベーカリーの線分図の部分が10になったので、同じ仲間として足し算や引き算ができるようになりました。
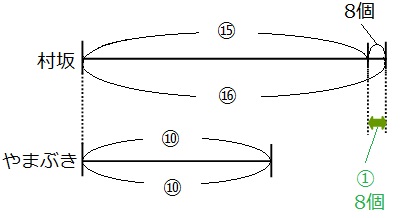
それでは線分図を見て、個数と比の両方がわかる部分を探しましょう。

上の線分図の緑の矢印の部分に注目してみましょう。

比→⑯－⑮＝①
個数→8個

なので、①が8個に当たることがわかりました。普段やまぶきベーカリーで作るメロンパンの数は⑩なので、

8個×⑩＝80個

よって答えは

80個

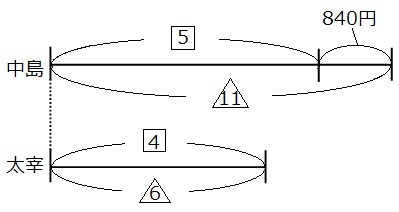
線分図を書いて見比べていきます。

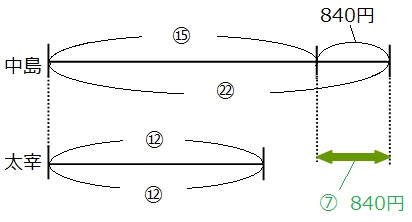
はじめの二人の所持金の差はわかりません。太宰さんの線分図の長さは変わっていません。ですので、太宰さんの線分図の比の数字を最小公倍数でそろえます。 □を3倍、△を2倍して、線分図を書き直してみましょう。

□も△も、太宰さんの線分図の部分が12になったので、同じ仲間として足し算や引き算ができるようになりました。
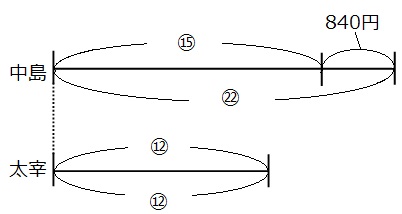
それでは線分図を見て、金額と比の両方がわかる部分を探しましょう。

上の線分図の緑の矢印の部分に注目してみましょう。

比→㉒－⑮＝⑦
金額→840円

なので、⑦が840円に当たることがわかりました。では、①に当たる金額を求めましょう。

840円÷⑦＝120円

これで、①が120円に当たることがわかりました。中島さんのはじめの所持金は⑮なので、

120円×⑮＝1800円

よって答えは

1800円

線分図を書いて見比べていきます。

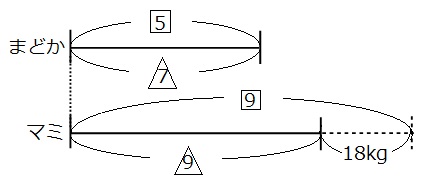
はじめの二人の体重の差はわかりません。まどかさんの線分図の長さは変わっていません。ですので、まどかさんの線分図の比の数字を最小公倍数でそろえます。 □を7倍、△を5倍して、線分図を書き直してみましょう。

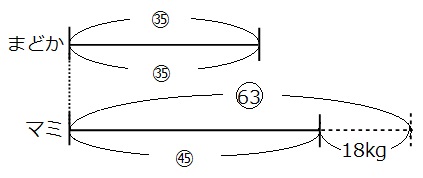
□も△も、まどかさんの線分図の部分が35になったので、同じ仲間として足し算や引き算ができるようになりました。
それでは線分図を見て、体重と比の両方がわかる部分を探しましょう。

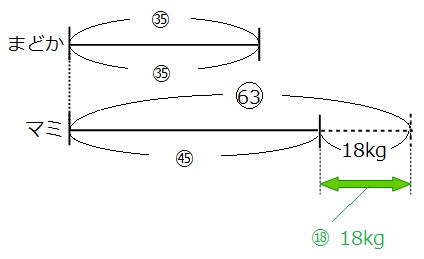
上の線分図の緑の矢印の部分に注目してみましょう。

比→63－45＝⑱
体重→18kg

なので、⑱が18kgに当たることがわかりました。では、①に当たる金額を求めましょう。

18kg÷⑱＝1kg

これで、①が1kgに当たることがわかりました。マミさんのダイエット後の体重は㊺なので、

1kg×㊺＝45kg

よって答えは

45kg