面積と辺の比
面積と比
中学受験の面積の問題では、比を使うことが多くなります。
面積の公式を使うだけでは解けないので、慣れるまでは大変かもしれません。
ですが、ある程度はパターンがあります。「こういう形が見えたら、こんなふうに解く。」みたいなやつです。
出題する方も、あの手この手を使って「こういう形」をカモフラージュしてきますが、根気よく探していけば必ず解けますので頑張ってください。
図形の面積の公式
そもそも図形の面積を求められなければ始まらないので、公式を並べて書いておきます。
正方形の面積(その1)=1辺×1辺
正方形の面積(その2)=対角線×対角線÷2
長方形の面積=たて×横
三角形の面積=底辺×高さ÷2
平行四辺形の面積=底辺×高さ
ひし形の面積=対角線×対角線÷2
台形の面積=(上底+下底)×高さ÷2
円の円周の長さ=直径×円周率
円の面積=半径×半径×円周率
おうぎ形の弧の長さと面積は、円の円周の長さや面積の公式にちょっと付け加えるだけです。
おうぎ形の弧の長さ
| = | 直径×円周率× | 中心角 | ||
| 360° |
おうぎ形の面積
| = | 半径×半径×円周率× | 中心角 | ||
| 360° |
比の計算
比の計算もたくさん出てきます。特に比例式は当然のように使っていくので、しっかりと練習をしておきましょう。 他にももうひとつ、よく使う計算方法があるので、例題で確認してみます。
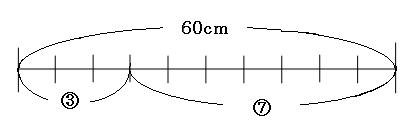
線分図にしてみます。
図のように、60cmを3:7に分けたので、目盛りは全部で10個になりました。1目盛りあたりの長さを出すと、
60cm÷10=6cm
左側は3目盛りなので、
6cm×3=18cm
右側は7目盛りなので、
6cm×7=42cm
よって答えは
18cmと42cm
ひとつの式にまとめて、
| 60cm× | 3 | = | 18cm | |
| 3+7 |
のように計算できるようにしておくと、楽に素早く求められます。
それでは、比を使った面積の問題を実際に解いていきましょう。
面積と辺の比とは
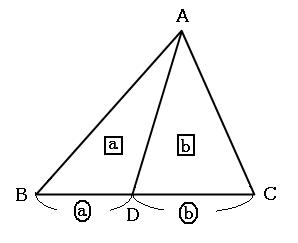
三角形の面積の公式が「底辺×高さ÷2」なので、「高さが等しければ、底辺の比と面積の比は同じになる」と考えられます。 この法則を使って面積を求めることができます。
このように、BDとCDの比(底辺の比)がa:bならば、三角形ABDの面積と三角形ACDの面積の比もa:bになります。
この形は非常によく出てきて何度も何度も使うのですが、名前がついていません。ここでは「テントの形」と名前をつけておきます。(←今思いついた)
テントの形が見えたら、「比を使って面積を求めるかも!」と思ってください。この法則をもう少し発展させます。
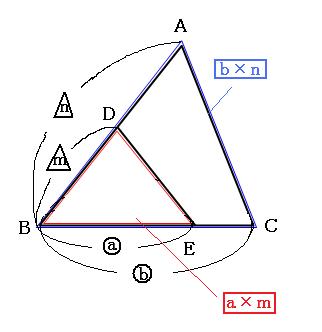
図のように、BE:BC=a:b、BD:BA=m:nならば、三角形DBE(赤い三角形)の面積:三角形ABC(青い三角形)の面積=(a×m):(b×n)になります。
こちらは位置関係がちょっと見にくくて間違いやすいので、しっかり練習しておいてください。
このパターンの図形にも名前がついていません。ここでは「ドリルの形」と名前をつけておきます。(←今思いついた。そして無理がある。)
すみません、良い名前が思いついたら教えていただけると助かります。
面積と辺の比の問題の解き方
実際の問題では、テントの形やドリルの形がタテ・ヨコ・ナナメにひっくり返ったり、巧妙に隠されてて見つけにくくなっていたりします。 なので、たくさん問題を解いて、いつでもどこでもテントとドリルを見つけられるように練習をしましょう。
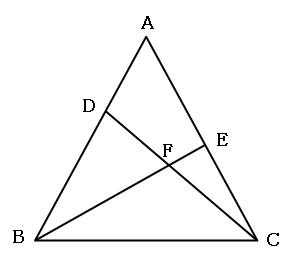
まずは問題文を読みながら、図に数字を書き込んでいきましょう。比は、○や□で数字で囲んでおくと間違いにくいです。
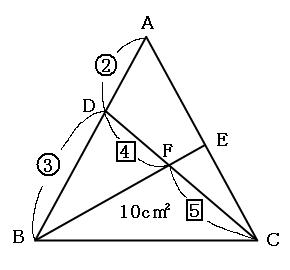
次に、下の図のテントの形の部分(赤い点線)に注目しましょう。
ひっくり返っていますが、テントの形です。テントの形の法則より、DF:FC=4:5なので、三角形BDFの面積:三角形BCFの面積も4:5になります。 三角形BCFの面積は10cm²なので、これをもとに比例式を作ると、
三角形BDFの面積:三角形BCFの面積=
4:5=a:10cm²
5×a=4×10
5×a=40
a=8
(比例式の解き方
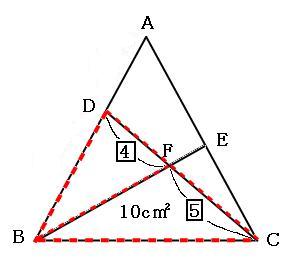
なので、三角形BDFの面積は8cm²です。さらに、三角形BDFと三角形BCFを合わせた三角形CBDの面積は、
8cm²+10cm²=18cm²
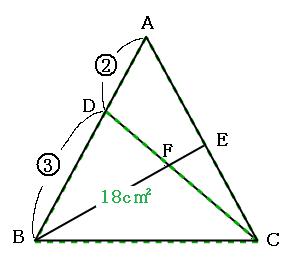
と、なります。次に、下の図のテントの部分(緑の点線)を見てみましょう。
テントの形の法則より、AD:DB=2:3なので、三角形CADの面積:三角形CBD=2:3。さらに三角形CBDの面積が18cm²なので比例式を作って、
2:3=b:18cm²
3×b=36
b=12
よって、三角形CADの面積は12cm²。これより三角形ABCの面積は、
三角形ABC=三角形CAD+三角形CBD
=18cm²+12cm²
=30cm²
よって答えは
30cm²
どうでしょう。ひっくり返ったりしていますが、テントの形を見つけられたでしょうか。
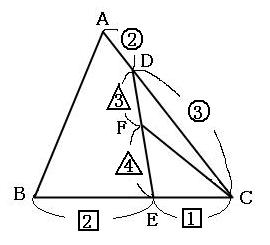
まずは問題文を読みながら、図に数字を書き込んでいきましょう。
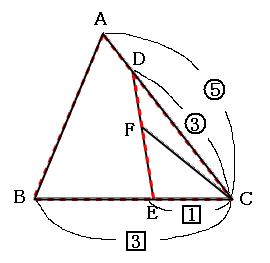
次に下の図のドリルの形の部分(赤い点線)に注目しましょう。ドリルの形の場合AD:DC=2:3のままでは見にくいので、AC:DC=5:3に書き直しておきます。 同じようにして、BC:EC=3:1に書き直しておきます。
ドリルの形の法則より、
三角形ABCの面積:三角形DECの面積=(3×5):(1×3)
=15:3
三角形ABCの面積は105cm²なので、これをもとに比例式を作ると、
15:3=105cm²:a
15×a=315
a=21
で、三角形DECの面積が21cm²であることがわかりました。
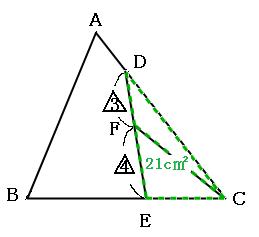
続いて、下の図のテントの形の部分(緑の点線)に注目してみましょう。
テントの形の法則より、三角形CDFの面積:三角形CFEの面積=3:4。 つまり、求めたい三角形CFEの面積は、21cm²を3:4に分けたうちの4の方なので、
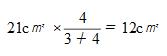
よって答えは
12cm²
ドリルの形は、見るべき比の場所を間違えないように気をつけてください。それでは面積と辺の比をまとめます。
これで難しい面積の問題の半分は解けます。(ちょっと盛った)次は残りの半分、合同と相似のお話です。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!