相似の問題② 平行四辺形の対角線を3つに分ける
平行四辺形の対角線を3つに分ける問題の解き方
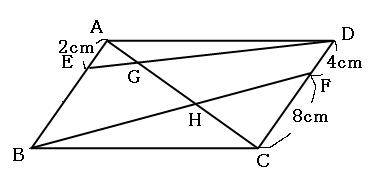
相似を使った図形の問題には、平行四辺形がよく登場するのですが、その平行四辺形の対角線を3つに分けなければならなくなることがあります。
少し手順は長くなりますが、基本はトンガリとチョウチョです。連比の考え方も使いますので、復習をしておいてください。
(トンガリとチョウチョについてはこちら)(連比についてはこちら)
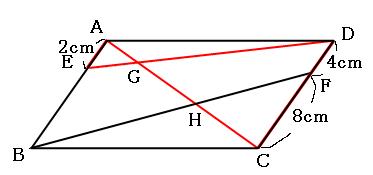
まずは、下の図の赤いチョウチョに注目してみましょう。
この赤いチョウチョは、辺AEと辺CDが平行なので(←四角形ABCDが平行四辺形だから)、三角形GAEと三角形GCDが相似になっています。
相似比を求めると、
辺AE:辺CD=2cm:12cm=1:6
よって、辺AG:辺CGも1:6です。
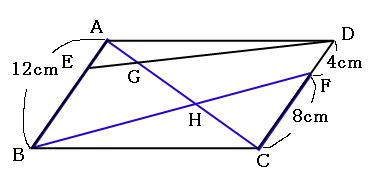
なお、四角形ABCDは平行四辺形なので、辺ABの長さと辺CDの長さは同じです。よって、辺ABの長さは12cmです。これをふまえた上で、下の図の青いチョウチョに注目します。
この青いチョウチョは、辺ABと辺CFが平行なので(←四角形ABCDが平行四辺形だから)、三角形HABと三角形HCFが相似になっています。
相似比を求めると、
辺AB:辺CF=12cm:8cm=3:2
よって、辺AH:辺CHも3:2です。
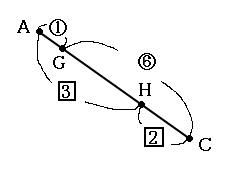
ここで線分ACだけ抜き出して書いてみます。ここまでで求めた、AG:CG=1:6と、AH:CH=3:2も書き込んでみます。
上の図を見ると、線分ACの長さが、○だと⑦、□だと5になっています。このままでは○と□の数字は計算できないので、どちらも最小公倍数の35になるようにします。 そのために、○は5倍、□は7倍します。そうしてさっきの図を書きなおしてみると、
上の図より、AG:GH:HC=5:16:14
よって答えは
5:16:14
ふたつのチョウチョと連比を使いました。少し手順が長いですが、ほとんどの場合はこのやり方で求められますので、頑張ってマスターしましょう。
3つに分ける線分が、平行四辺形の対角線でないときも手順は同じです。2種類の切り方でそれぞれ比を出して、連比を使ってひとつの比にまとめます。
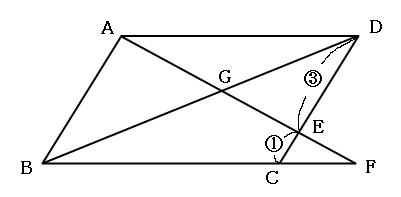
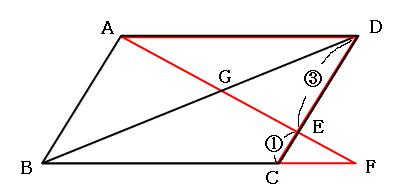
まずは、下の図の赤いチョウチョに注目してみましょう。
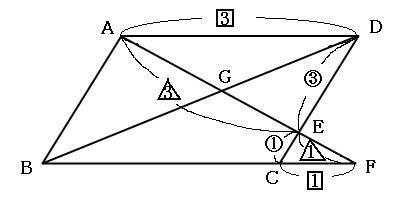
この赤いチョウチョは、辺ADと辺FCが平行なので、三角形EADと三角形EFCが相似になっています。相似比は3:1です。
したがって、EA:EFも3:1ですし、AD:FCも3:1です。
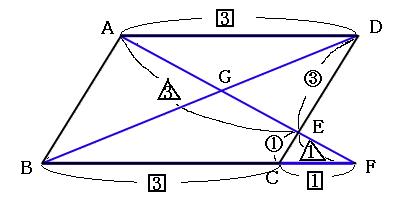
また、四角形ABCDが平行四辺形なので、辺ADと辺BCの長さは同じです。辺ADの長さが3なので、辺BCの長さも3です。 それをふまえた上で、下の青いチョウチョに注目してみましょう。
この青いチョウチョは、辺ADと辺FBが平行なので、三角形GADと三角形GFBが相似になっています。
相似比を求めると、
AD:FB=3:4
よって、GA:GFも3:4。
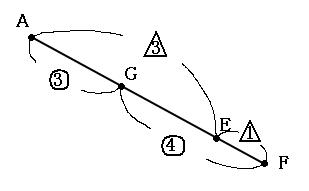
ここで線分AFだけ抜き出して書いてみます。ここまでで求めた、EA:EF=3:1と、GA:GF=3:4も書き込んでみます。
上の図を見ると、線分AFの長さが、変な形の○だと7、△だと4になっています。このままでは変な形の○と△の数字は計算できないので、どちらも最小公倍数の28になるようにします。 そのために、変な形の○は4倍、△は7倍します。そうしてさっきの図を書きなおしてみると、
上の図より、AG:GE:EF=12:9:7
よって答えは
12:9:7
この種類の問題は比がたくさん出てきて、○や□や△だけでは書ききれず、五角形や星形なんかも使って書き分けたりします。
今回は変な丸を使いましたが、自分のお気に入りの形とかを決めておくと、勉強中も少し遊べて楽しいと思います。
それでは、平行四辺形の対角線を3つに分ける相似の問題をまとめます。
ここまでできるようになれば、図形と比の問題はよく理解できていると思います。頑張りました!次は影の長さを出します。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!