相似の問題① トンガリとチョウチョ
チョウチョとは
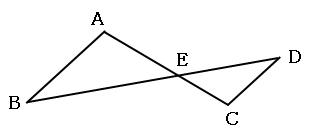
下の図のような形をチョウチョといいます。(私が勝手にチョウチョと名付けました。)
上の図で、辺ABと辺CDが平行ならば、三角形EABと三角形ECDは相似です。(相似の解説はこちら)
ただし、必ず辺ABと辺CDが平行でなければなりません。平行であることを確認し忘れて間違える人が多いので、気をつけましょう。
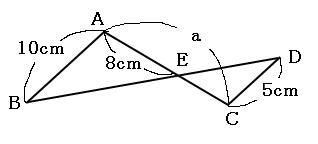
三角形EABと三角形ECDはチョウチョの形で、しかも辺ABと辺CDは平行なので、相似です。 対応する辺の組でどちらも長さがわかっているのは、辺ABと辺CDの組です。
辺AB:辺CD=10cm:5cm=2:1
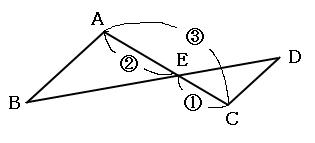
よって、ふたつの三角形の相似比は2:1です。だから、辺EA:辺ECも2:1です。なので、辺EA:辺ACは2:3になります。
これをもとに比例式を作ると、
2:3=8cm:a
2×a=24
a=12
(比例式の解き方)
よって答えは
12cm
トンガリとは
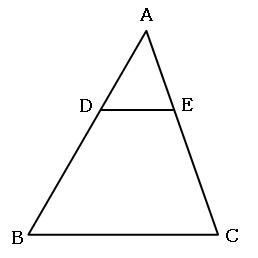
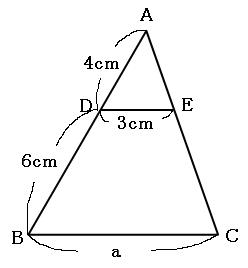
下の図のような形をトンガリといいます。(私が勝手にトンガリと名付けました。)
上の図で、辺DEと辺BCが平行ならば、三角形ADEと三角形ABCは相似です。 こちらも、必ず平行であることを確認してください。それと、チョウチョの形と比べて、三角形の位置関係を間違えやすいです。 繰り返しになりますが、相似なのは三角形ADEと三角形ABCです。間違えないようにしましょう。
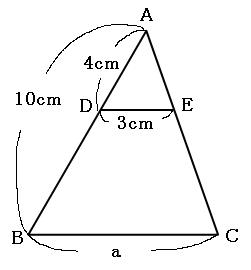
三角形ADEと三角形ABCはトンガリの形で、しかも辺DEと辺BCは平行なので、相似です。 対応する辺の組でどちらも長さがわかっているのは、辺ADと辺ABの組です。もう一度書きますが、辺ADと辺ABの組。決して辺ADと辺DBで比べないでください。 とても間違えやすいので注意してください。
辺AD:辺AB=4cm:10cm=2:5
よって、ふたつの三角形の相似比は2:5です。だから、辺DE:辺BCも2:5です。これをもとに比例式を作ると、
2:5=3cm:a
2×a=15
a=7.5
よって答えは
7.5cm
もう一度書きますが(←しつこい)、対応する辺の位置に注意してください。
なお、「トンガリ」の名前の由来は、ツメに装着して食べるあのお菓子です。あんまり似てないけど。
それでは、トンガリとチョウチョをまとめます。
次は、トンガリとチョウチョが混ざった問題を解いてみます。
トンガリとチョウチョは隠れている
ここまでで解説したトンガリとチョウチョですが、面積と辺の比の時と同じように、タテ・ヨコ・ナナメにひっくり返っていたり、巧妙に隠されていたりします。
いろいろな所に隠されているので、練習をたくさんして見つけられるようにしましょう。
先ほどからから何度も何度も書いていますが(←しつこい)、必ず平行であることを確認してからトンガリとチョウチョを使ってください。
逆に、問題文に「平行」という文字があったら「トンガリとチョウチョを使うかも。探してみよう!」と思うようにしましょう。
特に「平行四辺形」や「ひし形」という言葉にも反応してください。平行四辺形というだけで平行線が2組ありますので、トンガリチョウチョ率高いです!
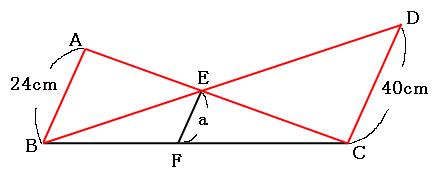
平行線が3本もあるので、「チョウチョとトンガリを探してみよう!」と思ってください。いくつか隠れているのが見つかると思いますが、まずは下の図の赤いチョウチョに注目します。
この赤いチョウチョは、辺ABと辺CDが平行なので、三角形EABと三角形ECDが相似になっています。(←必ず平行であることを確認してください!)
辺ABと辺CDの組は、どちらも長さが出ているので、
辺AB:辺CD=24cm:40cm=3:5
よって、ふたつの三角形の相似比は3:5です。
だから、辺BE:辺DEも3:5です。さらに、辺BE:辺BDは3:8です。
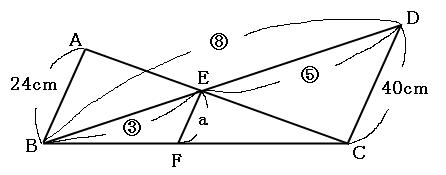
続いて、下の図の青いトンガリに注目してみましょう。
この青いトンガリは、辺EFと辺DCが平行なので、三角形BEFと三角形BDCが相似になっています。(←必ず平行であることを確認してください!)
ふたつの三角形の相似比は、
辺BE:辺BD=3:8
これをもとに比例式を作ると、
3:8=a:40
8×a=120
a=15
(比例式の解き方)
よって答えは
15cm
どうでしょう。トンガリとチョウチョを見つけられたでしょうか。今回は青いトンガリを使いましたが、もう一つの方のトンガリを使っても解けます。自分の見つけたものを使って大丈夫です。
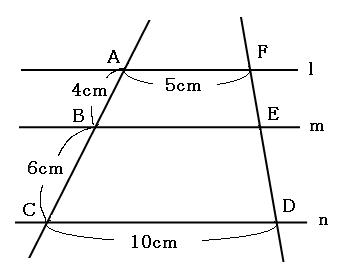
3本並んだ平行線の長さ
平行線が3本並んでいるときは、補助線を1本引いてトンガリを作ると求められることがあります。
平行線が3本もあるので、「チョウチョとトンガリを探してみよう!」と思ってください。が、どこを探しても見つかりません。そこで、補助線を1本引いてみましょう。
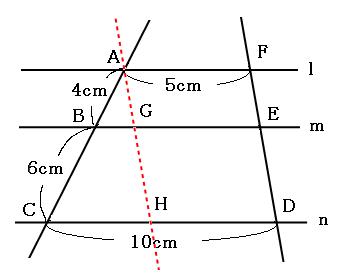
直線FDに平行で、点Aを通る直線を引きます。
すると、左の方にトンガリができました。辺BGと辺CHは平行なので、三角形ABGと三角形ACHは相似です。
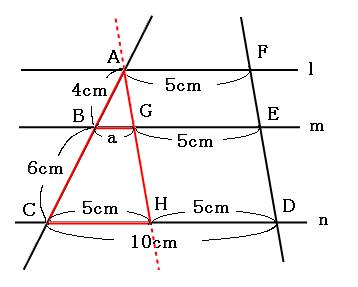
右の方には平行四辺形ができました。これをもとに、図に長さを書き加えてみます。
それでは、赤いトンガリを使って、辺BGの長さを出していきましょう。三角形ABGと三角形ACHの相似比は、
辺AB:辺AC=4cm:10cm=2:5
これをもとに比例式を作ると、
2:5=a:5cm
5×a=10
a=2
よって、辺BGは2cm。
辺BE=辺BG+辺GE
=2cm+5cm
=7cm
よって答えは
7cm
「平行線がたくさんあるのに、トンガリもチョウチョも見つからない!→そうだ、作ってしまおう!」の発想です。
ここまで思いつくようになれば、トンガリとチョウチョ探しマスターです。
それでは、トンガリとチョウチョ実践編をまとめます。
次も、もう少しチョウチョとトンガリで遊びます。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!