旅人算の解き方
旅人算とは
旅人算とは、逆向きに進む2人が途中で出会ったり、同じ向きに進む人に出会ったりする、速さの問題です。主な出題パターンは4つです。
- 2つの地点から2人が逆向きに進み、途中で出会う
- 前を進む人に、後ろから追いかけてきた人が追いつく
- 2人が池の周りを逆方向に回って、途中で出会う
- 2人が池の周りを同じ方向に回って、途中で追い越す
その他にも、時計の短針と長針の間の角度を求める「時計算」というものもあります。
旅人算の解き方
旅人算は2人が同時に動くので難しく見えますが、ポイントをしっかり押さえておけば簡単に解けます。特に押さえておきたいポイントは2つです。
- 出発時の状況と、ゴール時の状況を把握すること
- 時速なら1時間後、分速なら1分後、秒速なら1秒後のことを考える
それでは、例題を使って実際に4つのパターンを解いていきましょう!
旅人算① 出会う旅人算の解き方
ここでは、2人が別々の地点から逆向き出発して、出会うまでの時間を求める旅人算の解き方を解説します。少し前にも書きましたが、出発時とゴール時の状況、1分後(1時間後、または1秒後)の状況を考えるのがコツです。
サマルトリア城からサマルトリアの王子が、ローレシア城に向かって時速3kmで、ローレシア城からローレシアの王子が、サマルトリア城に向かって時速4kmで、同時に歩き始めました。
2人は出発してから何時間後に出会うでしょう。
速さの問題なので、とりあえず「みはじ」の図をどこかに書いておきましょう。
まずは状況を整理します。
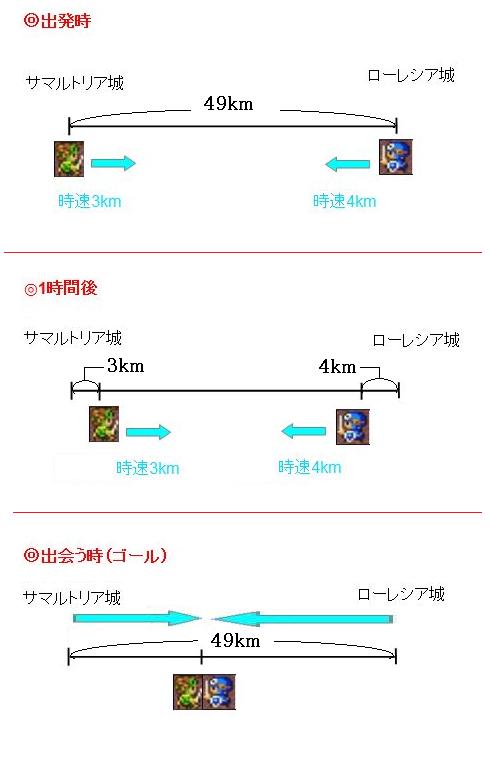
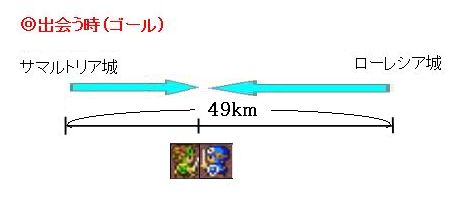
出発時、1時間後、出会う時を並べるとこんな感じです。まずは出会った時の状況を、もう一度確認してみましょう。
出会うまでに歩いた時間が分からないので、2人それぞれが歩いた道のりは分からないのですが、2人が歩いた道のりの合計は図を見ればわかります。 2人が歩いた道のりの合計は49km。サマルトリア城とローレシア城の間の距離と同じです。続いて、2人が歩き始めてから1時間後の状況をもう一度見てみましょう。
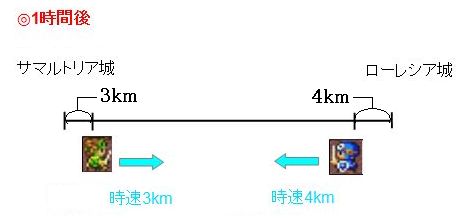
サマルトリアの王子が3km、ローレシアの王子が4km進んでいるので、2人合わせて1時間で3km+4km=7km進んでいます。
2人の道のりの合計が1時間で7kmなので、2人の道のりの合計が49kmになるのは、
49÷7=7
よって答えは
7時間後
すれ違わずに出会えて良かったですね!!ちなみに、1時間後の2人の道のりの合計を出した時に計算した3+4=7の計算は、2人の速さである時速3kmと、時速4kmの数字を足したものと同じになります。 速さは距離や時間とは違うので本当は足し算はできないのですが、あくまでも速さを足したように見えるということから、
逆向きに進んで出会うまでの時間=道のり÷速さの和
速さの和=道のり÷逆向きに進んで出会うまでの時間
道のり=速さの和×逆向きに進んで出会うまでの時間
と、覚えてしまう人もいます。さらにこれを「みはじ」の表にして、
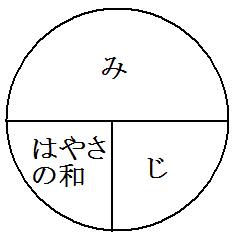
と、書いてしまう人もいます。あまりに公式に頼りすぎると応用が利かなくなってしまうので、単純に覚えてしまうのはおすすめしません。 まずはたくさん練習問題を解いて、手順を練習するのが良いと思います。それでは出会う系旅人算をまとめます。
続いて、追いつく系の旅人算の解き方を考えてみましょう。
旅人算② 追いつく旅人算の解き方
ここでは、先に進んでいる人に、後ろから追いかけてくる人が追いつくまでの時間を求める旅人算の解き方を解説します。 追いかける側が出発する瞬間の状況をしっかりと把握することがコツとなります。
速さの問題なので、とりあえず「みはじ」の図をどこかに書いておきましょう。
まずは状況を整理します。
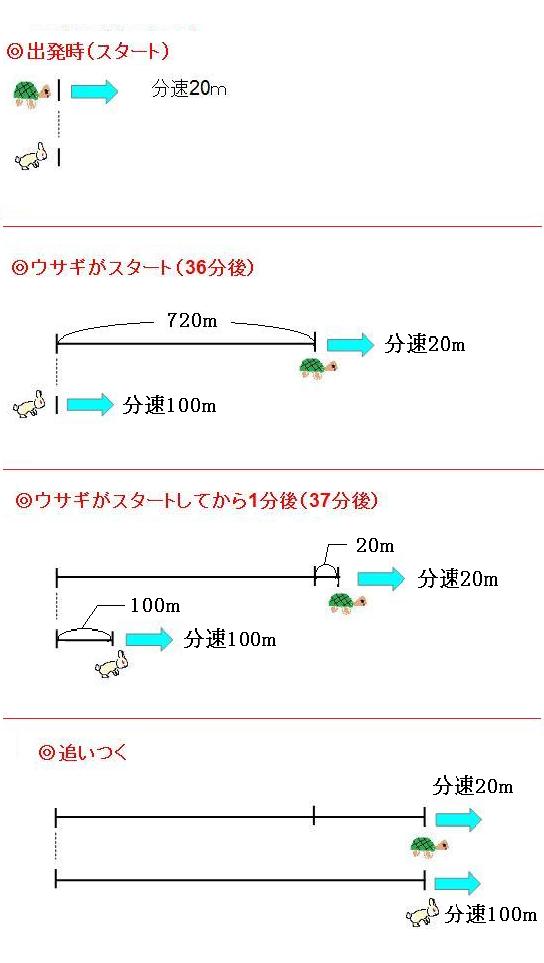
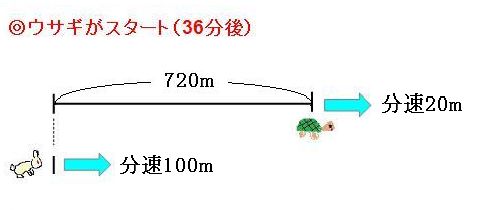
カメが出発した時、ウサギが出発した時、ウサギが出発してから1分後、ウサギがカメに追いつく時を並べるとこんな感じです。まずはウサギが出発した瞬間に注目します。
すでにカメが出発して36分が経っていますので、この間にカメが走った道のりは、
分速20m×36分=720m
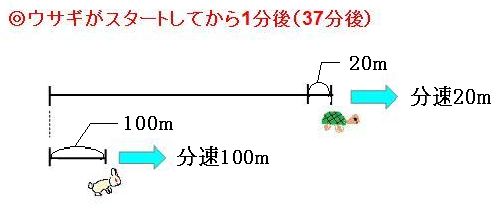
で、720m進んでいます。ウサギはこれから、この720mを追いつかなければなりません。では、ウサギが出発してから1分後に注目してみましょう。
この1分間で、カメは20m、ウサギは100m進みました。よって2人(1匹と1羽)の間は「100m-20m=80m」縮まりました。 720mあった2人(1匹と1羽)の間が、1分で80mずつ縮まるので、追いつくまでにかかる時間は、
720÷80=9分
よって答えは
9分後
カメとウサギの絵が思いの外上手に描けて、非常に満足です。それにしても、36分も頑張って作ったリードを、たった9分でウサギにうめられてしまうカメさんが可愛そうです。 なお、ウサギが出発してから1分で縮まった2人(1匹と1羽)の間(80m)ですが、この数字は2人(1匹と1羽)の速さの差と同じ数字になります。 出会う旅人算と同じように、速さは足したり引いたりはできないのですが、引き算をしたように見えるということから、
同じ向きに進んで追いつくまでの時間=2人の間の道のり÷速さの差
速さの差=2人の間の道のり÷同じ向きに進んで追いつくまでの時間
2人の間の道のり=速さの差×同じ向きに進んで追いつくまでの時間
と、覚えてしまう人もいます。さらにこれを「みはじ」の表にして、
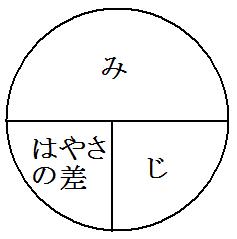
と、書いてしまう人もいます。ですが、こちらも単純に覚えてしまうことはあまりおすすめしません。それでは追いつく系の旅人算をまとめます。
続けて、池の周りを逆向きにグルグル回る系の旅人算の解き方を考えてみましょう。
旅人算③ 池の周りを逆向きに回って途中で出会う旅人算の解き方
「なぜ2人で池に来て、逆向きに回るのか!?普通は一緒に回るのではないか!?」
まったく意味の分からない設定ですが、なぜか算数の問題ではよく出題されます。一通り「なんでやねん。」とツッコミを入れてから、シブシブ出題者に付き合ってあげてください。
この系統の問題は、出会う旅人算の解き方とほぼ同じです。一直線だったものが円に変わっただけです。出会う旅人算がしっかりと定着していれば、とても簡単だと思います。
2人が出会うのは、出発してから何分後でしょう。
速さの問題なので、とりあえず「みはじ」の図をどこかに書いておきましょう。
「この2人(1頭と1匹)は一体何をやっているのだろう・・・」と思いながら、まずは状況を整理します。速さの単位が分速○mなので、池1周2kmも単位を「m」にそろえて、2000mに直しておきます。 (長さの単位変換のやり方はこちら)
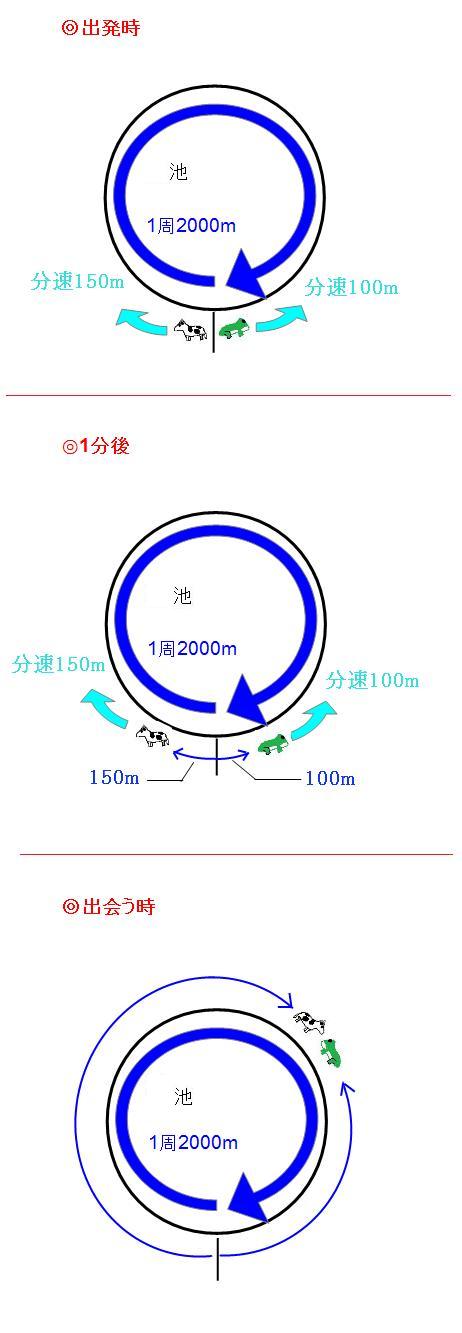
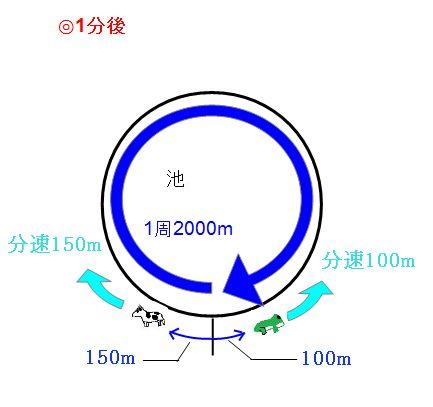
出発時、1分後、出会う時を並べるとこんな感じです。まずは、出会った時の状況をもう一度確認してみます。出会うまでのかかった時間がわからないので、ウシ君とカエル君それぞれが進んだ道のりはわからないのですが、2人(1頭と1匹)が進んだ道のりの合計は図を見ればわかります。 2人(1頭と1匹)が進んだ道のりの合計は2000mです。池1周の距離と同じです。続いて、出発してから1分後の状況を見てみましょう。
ウシ君が150m、カエル君が100m進んでいるので、2人(1頭と1匹)が進んだ道のりの合計は、
150m+100m=250m
1分間に2人(1頭と1匹)の進んだ道のりの合計が250mなので、2人(1頭と1匹)の進んだ道のりの合計が2000mになるのは、
2000÷250=8
よって答えは
8分後
ウシ君とカエル君の絵が上手に描けて、大変満足です。ちなみに、2度目に出会うのは更に8分後の16分後、3度目に出会うのは更に8分後の24分後、100回目に出会うのは8分×100回=800分後になります。 15時間歩き続ければ、100回もすれ違えますね!!
「池よりも外側を歩いてるんだから、実際歩いた道のりは、池の周りの長さよりも長いのではないか?」と思った方、そういう考えが思い浮かぶということは、問題をしっかりと理解できているということです。良いことです。 「池のふちのギリギリの所を歩くサバイバル系ゲームなんだな。」と思って、問題に付き合ってあげてください。 最初に書いた通り、手順は出会う旅人算と同じです。なので出会う旅人算と同じように、
池の周りを逆向きに進んで出会うまでの時間=1周の長さ÷速さの和
速さの和=1周の長さ÷池の周りを逆向きに進んで出会うまでの時間
1周の長さ=速さの和×池の周りを逆向きに進んで出会うまでの時間
と、覚えてしまう人もいます。こちらも、ただ暗記してしまうのはおすすめしません。 それでは、池の周りを逆向きに回って途中で出会う旅人算をまとめます。
すみません、出会う旅人算とまったく同じです。続いて、池の周りを同じ向きに回って途中で追い抜く旅人算の解き方を考えてみましょう。
旅人算④ 池の周りを同じ向きに回って途中で追い抜く旅人算の解き方
「なぜ池に2人で来て、違う速さで回るのか!?普通は一緒に回るのではないか!?」
こちらの問題も、「世の中にはおかしなことをする人たちもいるんだな。」と思いながら解いてあげてください。
この系統の問題は、追いつく旅人算の解き方と似ています。一直線だったものが円に変わって、少し見方が変わっただけです。追いつく旅人算がしっかりと定着していれば、難しくはないと思います。
フェラーリがプリウスを追い越すのは、出発してから何分後でしょう。
速さの問題なので、とりあえず「みはじ」の図をどこかに書いておきましょう。
まずは状況を整理します。単位がバラバラなので、「分」と「km」でそろえておきます。時速60km=分速1km、時速240km=分速4kmです。 (速さの単位変換のやり方はこちら)
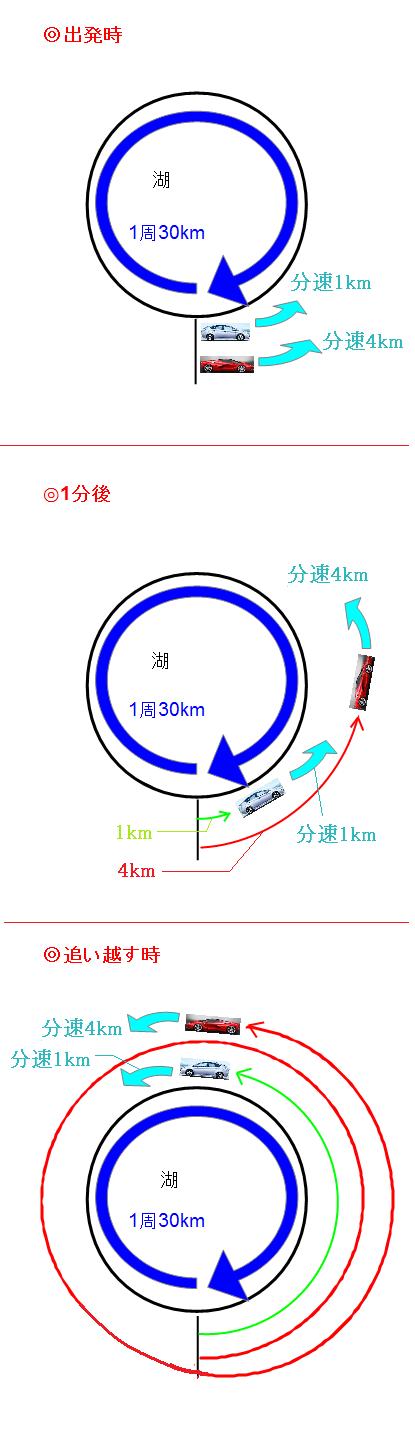
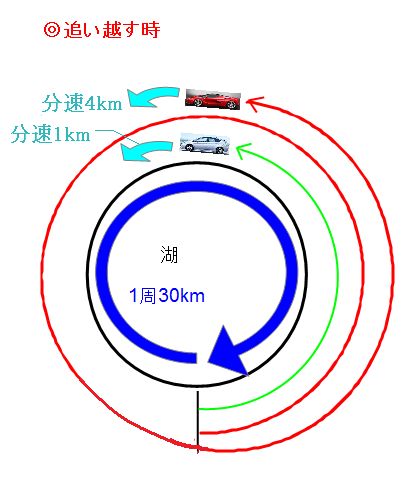
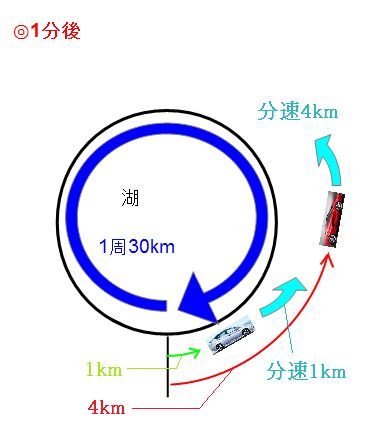
出発時、1分後、フェラーリがプリウスを追い越す時を並べるとこんな感じです。まずは、フェラーリがプリウスを追い越した瞬間に注目します。
追い越すまでの時間がわからないので、フェラーリとプリウスそれぞれが走った道のりはわからないのですが、図を見れば、フェラーリの方がプリウスよりも湖1周分(30km)多く走っているのがわかります。 続いて、スタートしてから1分後の状況を確認します。
最初の1分でプリウスは1km、フェラーリは4km進みました。つまり、フェラーリの方が「4km-1km=3km」多く走っていることになります。
プリウスよりフェラーリの方が1分間で3km多く走っているので、プリウスよりフェラーリの方が30km多く走るためには、
30÷3=10
よって答えは、
10分後
スピードの出し過ぎは危険です!ちなみに、2回目に追い越すのはさらに10分後の20分後、3回目に追い越すのはさらに10分後の30分後、100回追い越すのは10分×100回=1000分後になります。 16時間40分走り続ければ、プリウスを100回も周回遅れにできます。ただしガソリンがもたない。
最初に書いた通り、追いつく旅人算に考え方が似ています。なので、追いつく旅人算と同じように、
池の周りを同じ向きに回って追い抜くまでの時間=1周の長さ÷速さの差
速さの差=1周の長さ÷池の周りを同じ向きに回って追い抜くまでの時間
1周の長さ=速さの差×池の周りを同じ向きに回って追い抜くまでの時間
と、覚えてしまう人もいます。しつこいと思われるかもしれませんが、そのまま暗記してしまうのはおすすめしません。 それでは、池の周りを同じ向きに回って途中で追い抜く旅人算をまとめます。
続いて、旅人算に考えが似ている時計算の解き方を考えてみましょう。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!